Примеры действия упругой силы

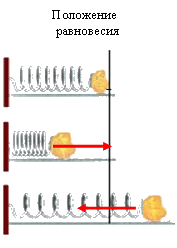
	Действующая на тело упругая сила со стороны деформированной пружины заставляет тело совершать колебания около положения равновесия
	Прыжок на упругом канате в грот. На человека со сторон каната действует сила упругости каната
Воздушные гимнасты. Сила тяжести, действующая на гимнастов, скомпенсирована упругой силой деформированных канатов
	Полет теннисного мяч обусловлен импульсом силы упругости, подействовавшей на него со стороны упруго деформированной сетки ракетки
	Прыжок спортсмена вверх обусловлен действием силы упругости со стороны деформированной доски

Гравитационные силы (силы тяготения). Гравитационное взаимодействие описывается законом всемирного тяготения, открытым Ньютоном в 1682 г. Ньютон получил свой закон, основываясь на трех законах Кеплера, установленных на основании астрономических наблюдений Тихо Браге за движением планет Солнечной системы. Согласно этим законам:

 траектории всех планет имеют форму эллипса, в одном из фокусов которого находится Солнце;

 площади, описываемые радиус-вектором планеты за равные промежутки времени, одинаковы;

 для всех планет отношение квадрата периода обращения к кубу большой полуоси эллипса имеют одно и то же значение:

.

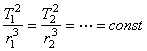Орбиты большинства планет мало отличаются от круговой. Рассмотрим две планеты, движущиеся вокруг Солнца по круговым орбитам. Сила, сообщающая планетам нормальное ускорение, согласно второму закону:

.

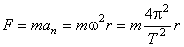Отношение сил, действующих на планеты, 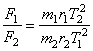. С учетом третьего закона Кеплера,

.

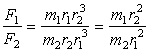Это соотношение, справедливое для любых планет, возможно, если

,

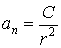где С – постоянная, одинаковая для всех планет, r – расстояние от планеты до Солнца. Постоянная С не зависит от массы планеты, а может зависеть от параметров, характеризующих Солнце. Но Солнце и планеты выступают во взаимодействии как равноправные тела, поэтому, если сила 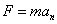пропорциональна массе планеты m, то она должна быть пропорциональна и массе Солнца М. На этом основании можно записать силу тяготения в форме

,

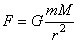(2.4)

где 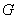– гравитационная постоянная. Так как Солнце и планеты отличаются только массами, то естественно считать, что это выражение применимо к определению силы взаимодействия между любыми телами.

Закон всемирного тяготения формулируется следующим образом: сила тяготения между двумя материальными точками пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними. Из формулы (2.4) видно, что гравитационная постоянная численно равна силе взаимного тяготения двух материальных точек, имеющих массы, равные единице массы, и находящихся друг от друга на расстоянии, равном единице длины. Числовое значение гравитационной постоянной установлено экспериментально. Впервые это сделал английский ученый Кавендиш с помощью крутильного динамометра (крутильных весов). В системе единиц СИ гравитационная постоянная имеет значение 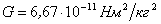. Следовательно, две материальные точки массой 1 кг каждая, находящиеся друг от друга на расстоянии 1 м, взаимно притягиваются гравитационной силой, равной 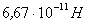. Изложенные соображения нельзя рассматривать как вывод закона всемирного тяготения, они являются лишь иллюстрациями к соображениям Ньютона.

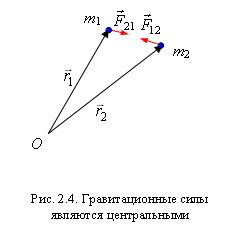
Гравитационные силы являются силами притяжения: на каждую массу действует сила притяжения со стороны другой массы. Таким образом, это всегда две силы, направленные по прямой, соединяющие их центры, поэтому эти силы являются центральными (рис. 2.4). В векторной форме силу, действующую на тело массой 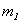со стороны тела массой 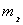, можно записать в следующем виде:

,

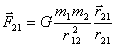где , .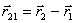

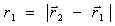Закон всемирного тяготения Ньютона справедлив только для точечных масс, то есть для таких тел, размеры которых малы по сравнению с расстоянием между ними. Однако его можно применить и для вычисления сил притяжения тел конечных размеров. Для этого нужно мысленно разбить тело на отдельные элементы, которые можно считать материальными точками, и затем векторно сложить все силы, создаваемые этими элементами. Именно таким способом можно показать, что закон Ньютона можно применить к однородным шарам, считая, что вся масса шара сосредоточена в его центре.

Основное физическое содержание второго закона Ньютона состоит в том, что сила гравитационного притяжения тел пропорциональна их инертным массам, то есть массам, характеризующим инертные свойства тел. Но инерция и способность к гравитационным взаимодействиям представляют разные свойства материи и, следовательно, гравитационное взаимодействие должно определяться гравитационными массами. Однако с высокой степенью точности экспериментально установлено равенство инертных и гравитационных масс.

Сила тяжести. Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. По закону всемирного тяготения она равна 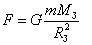. Тогда, согласно второму закону Ньютона:

,

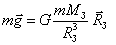где 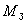– масса Земли; 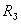– радиус Земли, 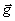– ускорение тела массой m. Таким образом, сила тяжести 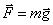. Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Модуль ускорения свободного падения g находят по формуле:

.

(2.5)

Из (2.5) следует, что ускорение свободного падения не зависит от массы падающего тела, то есть для всех тел в данном месте Земли оно одинаково. Поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. По этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле:

.

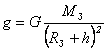Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 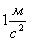. Следовательно, вблизи Земли (до высот порядка нескольких километров) сила тяжести практически не изменяется, а поэтому свободное падение тел вблизи Земли является движением равноускоренным.

Вес тела. Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору (или подвес), неподвижную относительно данного тела. Если сила тяжести является результатом взаимодействия тела с Землей, то вес тела появляется в результате совсем другого взаимодействия – взаимодействия тела и опоры (или подвеса). Поэтому вес обладает особенностями, существенно отличающими его от силы тяжести. В частности, эти силы приложены к разным телам, и, кроме того, вес существенно зависит от ускорения, с которым движутся совместно опора (подвес) и тело.

Гравитационное поле. Закон всемирного тяготения основан на теории дальнодействия, согласно которой действие одного тела на другое передается мгновенно (то есть с бесконечно большой скоростью) без участия среды. Согласно современным представлениям всякое взаимодействие тел на расстоянии осуществляется посредством материальной среды, называемой полем, и передается с конечной скоростью, которая не может быть больше скорости света. Гравитационное взаимодействие между телами, описываемое законом всемирного тяготения, осуществляется посредством гравитационного поля (поля тяготения). В каждой точке поля тяготения на помещенное туда тело действует сила тяготения, пропорциональная массе этого тела. Сила тяготения не зависит от среды, в которой находятся тела.

С этих позиций гравитационное взаимодействие представляется следующим образом. Всякое тело массой М создает вокруг себя гравитационное поле. Если в какую-либо точку поля поместить пробную массу m, то на нее будет действовать сила F, зависящая от свойств поля в этой точке и от величины массы пробного тела m.

Для количественной характеристики поля тяготения вводится физическая величина, называемая напряженностью гравитационного поля g. Напряженность гравитационного поля численно равна силе, действующей на единичную массу, помещенную в данную точку поля:

.

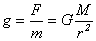Таким образом, напряженность гравитационного поля зависит только от массы М тела, создающего поле, и от расстояния от этого тела до точки наблюдения, но не зависит от массы пробного тела m. По величине напряженность гравитационного поля совпадает с ускорением свободного падения пробного тела.

Первая космическая скорость. Для того чтобы тело двигалось вокруг Земли по круговой орбите, сила тяготения должна сообщать ему нормальное ускорение :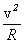

.

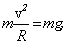Отсюда 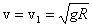. Скорость 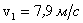называют первой космической скоростью. Приведенное значение получается, если принять g = 9,8 м/с, а радиус Земли R = 6370 км. Такое движение возможно, когда нет сил сопротивления воздуха, то есть на высоте более 100 км.

Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики.

Date: 2015-09-17; view: 1420; Нарушение авторских прав