Закон сохранения импульса

Импульс системы материальных точек под действием внешних сил изменяется. Согласно второму закону Ньютона, скорость изменения импульса равна равнодействующей внешних сил:

.

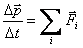(3.1)

Система материальных точек, на которую не действуют внешние силы, или действие внешних сил скомпенсировано, называется замкнутой. В этом случае уравнение (3.1) принимает вид 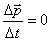, и, следовательно, импульс системы при движении не изменяется со временем: 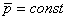. Таким образом, если геометрическая сумма внешних сил, действующих на систему материальных точек, равна нулю, то импульс системы сохраняется, то есть не меняется со временем. При этом импульсы отдельных частиц замкнутой системы могут меняться со временем. Однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Другими словами, отдельные части замкнутой системы могут только обмениваться импульсами. Сказанное справедливо, разумеется, только по отношению к инерциальным системам отсчета.

Так как полный импульс системы материальных точек 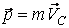, то для замкнутой системы материальных точек закон сохранения импульса утверждает, что центр масс системы движется равномерно и прямолинейно.

Может случиться, что система материальных точек или отдельная материальная точка не изолированы, но внешние силы действуют лишь в определенных направлениях, а в других отсутствуют. Тогда соответствующим выбором системы координат можно добиться, что одна или две проекции внешних сил обращаются в нуль. Пусть, например, нет сил, действующих в направлениях, параллельных плоскости 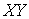, то есть 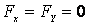, 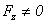. Тогда уравнение движения (3.1), записанное в проекциях на оси выбранной системы координат, имеет следующий вид:

.

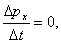
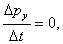
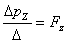Из этих уравнений следует, что 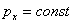, 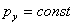. Это означает, что импульс системы в направлениях, параллельных плоскости 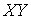, сохраняет свое значение.

Например, импульс свободно падающего тела не может сохраняться, так как на тело действует сила тяжести. Под действием этой силы вертикальная составляющая импульса непрерывно изменяется. Однако горизонтальная составляющая импульса при свободном падении остается неизменной.

Для материальной точки закон сохранения импульса означает, что в отсутствие внешних сил она движется с постоянной скоростью по прямой линии.

Date: 2015-09-17; view: 345; Нарушение авторских прав