Работа и энергия

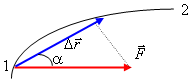Рис. 3.2. К определению работы

Пусть частица под действием силы совершает перемещение по некоторой траектории из положения 1 в положение 2 (рис. 3.2). В общем случае сила в процессе движения может меняться как по модулю, так и по направлению. Пусть частица совершила элементарное перемещение 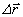, в пределах которого силу можно считать постоянной. Действие силы на перемещении 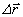характеризуют величиной, равной скалярному произведению 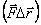, которую называют элементарной работой силы на перемещении :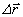

.

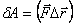(3.3)

Ее можно представить в другом виде:

,

где 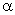– угол между векторами и 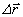, 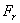– проекция вектора на направление вектора 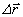. Поскольку перемещение 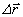предполагается малым, величина 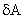называется элементарной работой в отличие от работы на конечном перемещении.

Величина 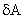– алгебраическая: в зависимости от угла 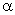(или знака проекции 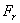) она может быть как положительной, так и отрицательной, и, в частности, равной нулю, если сила перпендикулярна перемещению .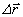

Рассмотрим одномерный случай, когда сила действует вдоль оси и движение происходит вдоль этой оси. Тогда при смещении материальной точки на сила совершает элементарную работу 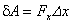. Если точка смещается из положения 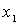в положение 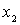, а сила при этом не является постоянной, то для вычисления работы необходимо весь интервал между точкам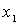и и 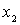разбить на столь маленькие отрезки 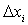, чтобы на каждом из них силу можно было считать постоянной и равной некоторому значению 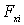(при этом неважно, в какой точке интервала берется значение 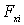). Элементарная работа на участке 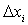равна , а полная работа при перемещении материальной точки из положения 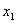в положение 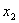определится как сумма работ на всех элементарных перемещениях:

.

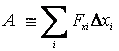Если устремить длины всех интервалов к нулю, а их количество – к бесконечности, получим точное значение работы:

.

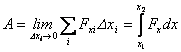(3.4)

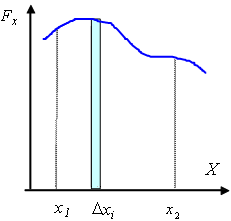Рис. 3.3. К расчету работы силы

Интеграл представляет сумму элементарных работ, которые совершаются при элементарных перемещениях, Из рис. 3.3 видно, что элементарная работа на перемещении 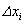численно равна площади заштрихованной полосы. Полная работа силы при перемещении материальной точки из 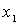в 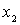будет равна площади фигуры, ограниченной кривой 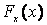, вертикальными прямыми, проходящими через точк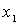и и 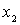, и осью . В этом заключается геометрический смысл интеграла, стоящего в правой части равенства (3.4).

Поскольку работа получается суммированием по многим состояниям системы, то в общем случае работа зависит от того, как меняется состояние. Иными словами работа, совершаемая при перемещении частицы, в общем случае зависит от формы ее траектории.

Если на частицу действует не одна, а несколько сил, то результирующая сила будет равна геометрической сумме всех действующих сил 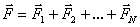, а работа этой силы на элементарном перемещении 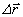определится соотношением 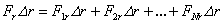. Следовательно, 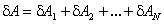. Таким образом, элементарная работа результирующей нескольких сил равна сумме элементарных работ этих сил. Очевидно, что это же утверждение справедливо и для работ на конечных перемещениях: .

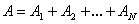Единицей работы в системе СИ является джоуль. Джоуль – работа силы в один ньютон на перемещении в один метр при условии, что направление силы совпадает с направлением перемещения: .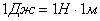

Для характеристики быстроты, с которой совершается работа, вводят величину, называемую мощностью. Мощность – это работа, совершаемая за единицу времени:

.

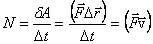В пределе при 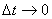мощность можно записать следующим образом:

.

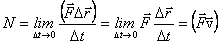Мощность измеряется в ваттах: 1 Вт = 1 .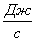

Date: 2015-09-17; view: 280; Нарушение авторских прав