Связь Qр и QV

Q_p = Q_V + DnRT

Энтальпия оказывается весьма удобной для анализа тепловых эффектов химических реакций.

Термохимия. Все химические реакции протекают с выделением или поглощением тепла; изучением тепловых эффектов реакций занимается одним из разделов физической химии – термохимия. Проявление тепловых эффектов при химических реакциях связано с разрывом одних химических связей и возникновением других. Разница в энергиях образующихся связей и тех, которые претерпели разрыв, проявляется в виде результирующего теплового эффекта данного химического процесса. Тепловой эффект реакции обычно относят к 1 моль конечного продукта.

Основой термохимии является закон Гесса: тепловой эффект химической реакции определяется только природой, составом и агрегатным состоянием исходных веществ и продуктов реакции и не зависит от возможных промежуточных химических стадий, т.е. от способа перехода от исходного состояния к конечному (при Р = const или V = const).

Неизвестные тепловые эффекты Q_р (где Q_p = DH) произвольных химических реакций можно рассчитать при помощи так называемых термохимических уравнений. Последние представляют собой обычные стехиометрические уравнения химических реакций, дополненные указанием агрегатного состояния всех веществ и численным значением теплового эффекта для данной реакции. Термохимическими уравнениями можно оперировать как уравнениями алгебраическими, т.е. складывать их, вычитать, умножать на постоянный множитель и др. Тогда для нахождения неизвестной теплоты какой-либо заданной реакции обычно производят операции комбинирования термохимических уравнений с уравнениями других подходящих реакций, для которых уже известны численные данные по тепловым эффектам (берутся из таблиц). Результатом такой процедуры является получение конечного уравнения искомой реакции с уже найденным (при комбинировании с привлеченными дополнительными уравнениями) численным значением ее теплового эффекта.

Тепловой эффект процесса зависит от температуры. В соответствии с законом Кирхгофа, изменение теплового эффекта с температурой равно разности теплоемкости продуктов реакции и теплоемкости исходных веществ.

Теплоемкостью (С_р) называется отношение количества сообщенной системе теплоты к наблюдаемому при этом повышению температуры. Для нахождения теплового эффекта DH₂ при температуре Т₂ надо знать DH₁ при температуре Т₁ и иметь данные по температурной зависимости теплоемкостей веществ, участвующих в реакции, в интервале температур от Т₁ до Т₂. Последние находятся обычно экспериментальным путем и описываются уравнениями в форме степенного ряда.

Так, если разность теплоемкостей продуктов реакции и исходных веществ 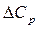= const, то

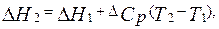(2.9)

где 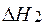– линейная функция температуры.

Второй закон термодинамики. Этот эмпирический закон не имеет единой формулировки, некоторые приведены ниже:

1. Невозможен самопроизвольный (естественный, спонтанный) переход энергии (в форме теплоты) от менее нагретого тела к более нагретому.

Перенос теплоты от холодного тела к горячему связан с компенсацией, т.е. с необходимостью дополнительной затраты работы, которая переходит в конечном счете в теплоту, поглощаемую горячим телом (так, в домашнем холодильнике происходит перенос теплоты от предметов к деталям прибора, а затем и в воздух; этот перенос требует затраты электроэнергии). Процессы, реализация которых связана с компенсацией, называются необратимыми.

2. Невозможно создать вечный двигатель 2-го рода. Тепло океана, например, может быть превращено в работу (согласно первому закону термодинамики), однако только при наличии соответствующего холодильника (согласно второму закону термодинамики).

3. Даже при обратимом течении реакции в работу может перейти только часть теплоты процесса. Другая часть, не превращенная в работу, передается при этом от более нагретых к более холодным частям системы.

Применительно к химическим реакциям (при Р = const, Т = const) этот закон можно выразить математически:

DH = DG + TDS или DG = DH – TDS, (2.10)

где DH₂ – тепловой эффект реакции, наблюдаемый при ее необратимом течении;

DG₂ – изменение свободной энергии Гиббса, или изменение изобарно-изотермического потенциала, т.е. это та максимальная часть энергии системы, которая в данных условиях может превратиться в полезную работу. При DG < 0 реакция протекает самопроизвольно.

DS – энтропия.Энтропия является функцией каждого конкретного состояния системы и не зависит от пути (например, какие промежуточные стадии проходит система при переходе из состояния 1 в состояние 2 для достижения нового состояния).

Произведением TDS определяется переносимое Q, которое не может быть превращено в работу даже при обратимом ходе реакции (величина «связанной энергии»). Это произведение показывает количество внутренней энергии, теряемой системой в форме теплоты:

TDS = Q или DS = Q / T, (2.11)

где DS = S₂ – S₁ – изменение энтропии системы при реакции, равное сообщенному системе теплу, деленному на абсолютную температуру, при которой система эту теплоту получает (отдает).

Кроме термодинамического потенциала – свободной энергии Гиббса (G), в термодинамике в качестве вспомогательной функции для описания процессов большое значение имеет и другой введенный термодинамический потенциал – свободная энергия Гельмгольца (F), или изохорно-изотермический потенциал,

DF = DUG – TDS (2.12)

В результате самопроизвольных процессов совершается работа, и когда эта возможность исчерпывается наступает равновесие. Поскольку самопроизвольным процессам соответствуют отрицательные изменения DF и DG, то знак изменения функции G (при P = const, Т = const) или функции F (при V = const, Т = const) и будет показывать возможность или невозможность самопроизвольного протекания реакции. Если изменения этих функций для состояний системы 1 и 2 равны нулю, то система находится в равновесии. Изобарно-изотермический потенциал реакции рассчитывается так же, как и тепловой эффект реакции – по стандартным теплотам образования веществ:

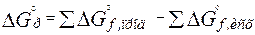. (2.13)

Для расчета 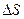любой реакции надо из суммы энтропий образования продуктов вычесть сумму энтропий образования исходных веществ (с учетом стехиометрических коэффициентов). Так, для стандартных условий:

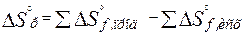. (2.14)

4. Самопроизвольно (следовательно, необратимо) в изолированной системе могут протекать только те процессы, которые связаны с увеличением энтропии, т.е. система из менее вероятного состояния переходит в наиболее вероятное и достигает такого макроскопического состояния, которому соответствует наибольшее число микроскопических состояний. Другими словами, процессы бывают самопроизвольными, когда конечное состояние может быть реализовано большим числом микросостояний и энтропия является мерой стремления системы к равновесию. Такие процессы должны сопровождаться увеличением энтропии.

Если для изолированных систем найденное значение DS положительное (DS > 0), то это является признаком самопроизвольности процесса, т.е. осуществление процесса возможно.

При DS < 0 самопроизвольное (без внешних воздействий) осуществление процесса невозможно, т.е. невозможен переход тепла от одного тела к другому телу с более высокой температурой.

Для равновесного процесса DS = 0 энтропия отличается от других параметров состояния системы (Р, Т, V) тем, что ее численное значение и значения ее изменения не поддаются непосредственному измерению и могут быть получены только косвенным, расчетным путем.

Можно сказать (принцип Больцмана), что энтропия – это мера вероятности пребывания системы в данном состоянии, а само содержание второго закона термодинамики обусловлено молекулярной природой и структурой вещества. Поскольку для неупорядоченного состояния термодинамическая вероятность всегда больше, чем для упорядоченного, то и энтропию, связанную с этой вероятностью, часто рассматривают как количественную меру хаотичности атомно-молекулярной структуры вещества. Так, найдено, что значение энтропии увеличивается: с ростом молекулярной массы в ряду веществ-аналогов; при реакциях, протекающих с увеличением числа молекул; при фазовых переходах от твердого к жидкому и от жидкого к газообразному состоянию и др.

Для неизолированной системы критерии возможности протекания процесса остаются теми же, но требуется знание общего изменения энтропии уже для новой термически изолированной системы (т.е. с учетом источника тепла).

Таким образом, критериями возможности самопроизвольного протекания процесса являются:

1. DS > 0 (изолированная система);

2. DF < 0 (V = const, T = const);

3. DG < 0 (Р = const, Т = const).

Если термодинамика дает отрицательный ответ на вопрос о возможности самопроизвольного протекания процесса, это означает, что без внешнего подвода энергии процесс невозможен (например, фотосинтез возможен только под воздействием солнечной энергии).

DG и DH имеют размерность Дж (кДж)/моль (для продуктов питания кДж/кг); DS – Дж/К·моль (энтропийная единица, э.е.); теплоемкость – Дж/К·моль.

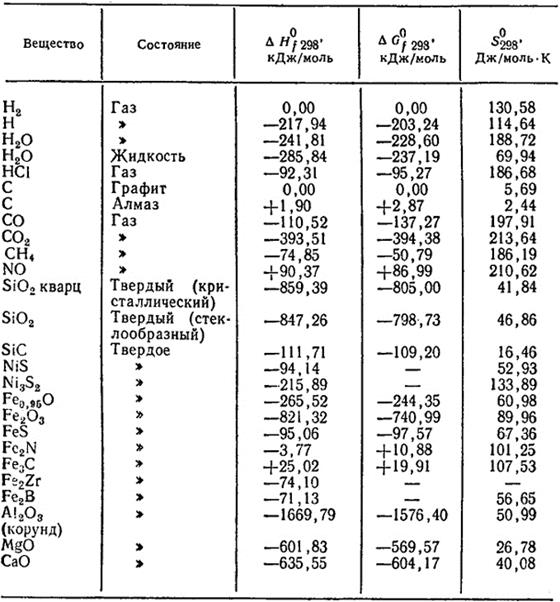
Расчет DG^о и DН^о производится с использованием имеющихся в справочниках значений:

D S^o₂₉₈, D G^o₂₉₈ и D Н^о₂₉₈ – образования химических соединений.

Таблица 1.1. Стандартные термодинамические величины некоторых веществ и энергии связи

Date: 2015-09-17; view: 594; Нарушение авторских прав