Связь между магнитным полем и электрическим током. Закон Био-Савара-Лапласа. Закон полного тока

Вспомним основные сведения, касающиеся магнитного поля. Магнитное поле характеризуется двумя векторными величинами: напряжённостью 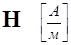и магнитной индукцией .

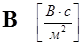Связь между ними дается уравнением 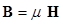, где μ – магнитная проницаемостьсреды, в которой рассматривается магнитное поле 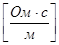. μ – скалярная величина для изотропнойсреды и тензорная величина для анизотропной среды.

Для воздуха и пустоты справедливо следующее уравнение: ,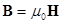

μ₀ = 4 π× 10^-7 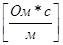- магнитная постоянная.

μ характеризует реакцию среды на внешнем магнитном поле.

Если 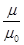< 1, то среда диамагнитная (как идеальный диамагнетик ведет себя сверхпроводящий материал, для которого = 0).

Если ≥ 1, то имеем дело с парамагнетиком; для ферромагнитных материалов, например, для электротехнической стали, - >> 1.

Магнитное поле создаётся электрическим током. Связь между указанными величинами в пустоте описывается законом Био-Савара-Лапласа (рис. 10.1).

.

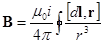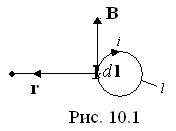Более универсален закон полного тока. Он имеет силу как в пустоте, так и в среде, содержащей вещества (например, ферромагнетики)

.

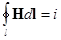Интеграл вектора 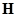вдоль замкнутого контура «l» (рис. 10.2) равен току, охваченному этим контуром. Направление интегрирования и тока в уравнении закона полного тока должны удовлетворять правилу правого винта.

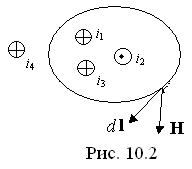Закон полного тока для данного случая записывается следующим образом:

.

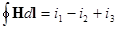Пример. Записать выражение для напряженности магнитного поля, созданного линейным током 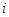(рис. 10.3).

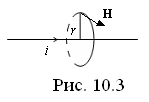
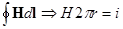, отсюда .

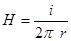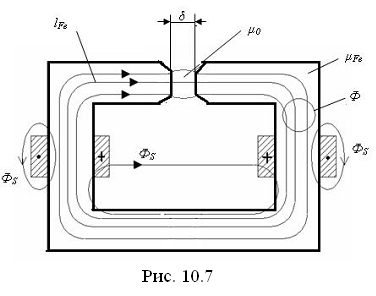
В основе расчёта магнитных цепей лежат два понятия: МДС или намагничивающая сила (F) и магнитный поток МДС (Ф). Под МДС вдоль замкнутого контура «l» понимается интеграл вектора 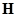вдоль этого контура, т.е.

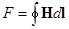
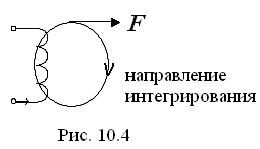
Согласно закону полного тока F равна току, охваченному этим контуром. Обычно для получения необходимого магнитного поля в качестве источников используют обмотку (катушку) с током. Если контур 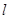охватывает такую обмотку с числом витков «w» (рис. 10.4), то МДС вдоль замкнутого контура равна .

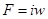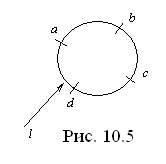
Контур можно представить как совокупность отдельных участков (рис. 10.5). В связи с этим МДС вдоль замкнутого контура можно представить как сумму МДС на отдельных участках:

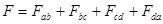
Под магнитным потоком сквозь площадку S (рис. 10.6) понимается поток вектора 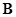сквозь эту площадку, т.е.

.

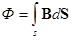10.2. Законы и параметры магнитных цепей

Под магнитной цепью понимается совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую цепь, по которой при наличии МДС замыкаются линии магнитной индукции.

а) Закон Ома (магнитный).

Рассмотрим постоянную магнитную цепь (рис. 10.7), содержащую ферромагнитный сердечник с воздушным зазором (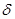) и две катушки, насаженные на сердечник. Нарисуем картину магнитного поля.

Поток Ф назовём главным (рабочим) магнитным потоком, Ф_S – потоком рассеяния. Поскольку магнитная проницаемость ферромагнитного сердечника значительно выше магнитной постоянной (~10³ - 10⁴), то при малом воздушном зазоре большая часть магнитных линий замыкается по сердечнику и лишь небольшая часть этих линий ответвляется в воздух, образуя, так называемый, поток рассеяния (Ф_S). К слову сказать, что Ф>>Ф_S. В связи с этим, Ф_S можно пренебречь. Кроме того, не будем учитывать выпучивание поля в воздушном зазоре. Тогда магнитный поток оказывается одинаковым во всех сечениях ферромагнитного сердечника и воздушного зазора, перпендикулярных магнитным линиям. Поэтому по аналогии с электрической цепью можно ввести понятие магнитной цепи. В этой цепи действуют две физические величины: магнитный поток Ф и создающие его МДС катушек, равные iw, где w – число витков обоих катушек, i – ток в них.

По аналогии с законом Ома для электрической цепи:

,

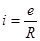запишем закон Ома для магнитной цепи в виде:

.

Назовём R_м магнитным сопротивлением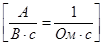

Найдём выражение для R_м. Всю МДС вдоль замкнутой магнитной цепи можно представить в виде суммы МДС на отдельных разнородных участках. В данном случае имеем два таких участках: ферромагнитный сердечник с длиной – l_Fе и воздушный зазор длиной δ. Поперечные сечения этих участков одинаковы и равны друг другу.

Итак .

Согласно формуле ,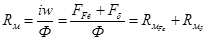

где 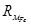- магнитное сопротивление ферромагнитного сердечника, 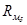- магнитное сопротивление воздушного зазора. Вычислим эти величины.

,

.

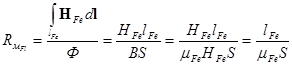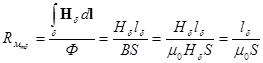Итак, в общем виде имеем формулу: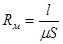

Таким образом, магнитное сопротивление участка магнитной цепи пропорционально средней длине этого участка и обратно пропорционально магнитной проницаемости и сечению этого участка.

б) Законы Кирхгофа (магнитные).

Участок магнитной цепи, в любом поперечном сечении которого Ф имеет одно и тоже значение, называется ветвью, точки, где сходятся не менее трёх ветвей – узлы.

Рассмотрим разветвлённую магнитную цепь. На рис. 10.8 представлена цепь с двумя узлами А и В и тремя ветвями ВСА; АВ и ADB

В каждом узле сумма магнитных потоков равна 0, т.е.

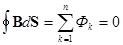- I закон Кирхгофа (магнитный).

Это аналогично уравнению для узла электрической цепи, составленному по первому закону Кирхгофа .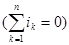

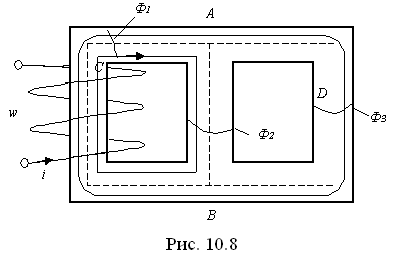
В рассмотренной схеме .

Для любого замкнутого контура магнитной цепи имеем:

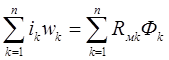- II закон Кирхгофа (магнитный),

т.е. сумма МДС, действующих в замкнутом контуре, равна сумме произведений магнитного сопротивления на магнитный поток во всех ветвях, входящих в этот контур. Это аналогично уравнению для контура электрической цепи, составленному по второму закону Кирхгофа .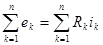

В рассмотренном случае для двух контуров имеем:

, ,

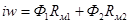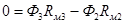где ; ; .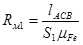

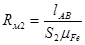Если магнитная цепь - сложная с «p» ветвями и «q» узлами, то число независимых уравнений будет равно «p», из них (q- 1) уравнений для узлов и p- (q- 1) уравнений для контуров.

Таким образом, расчёт магнитных цепей при пренебрежении потоками рассеяния аналогичен расчёту нелинейных электрических цепей. При этом магнитный поток Ф соответствует току i; МДС (iw) – ЭДС (), магнитное сопротивление R_м – электрическому сопротивлению R.

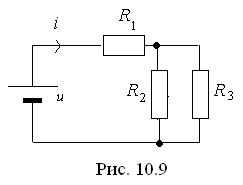Электрическая цепь, аналогичная приведённой магнитной цепи, показана на рис. 10.9.

Приведенная аналогия магнитных и электрических цепей формальна. По физическому содержанию законы Ома для магнитных и электрических цепей различаются между собой. В электрической цепи возможно существование постоянной ЭДС без того, чтобы под её действием возникал ток. Напротив, существование МДС всегда связано с одновременным существованием магнитного потока.

Сформулированные законы магнитной цепи, т.е. законы Ома и Кирхгофа, справедливы как для линейных, так и нелинейных магнитных цепей.

Линейными магнитными цепями называются цепи, магнитные сопротивления которых не зависят от напряжённости магнитного поля, т.е. эти сопротивления постоянны. Поэтому расчёт магнитных потоков в таких цепях проводится так же, как и расчёт токов в линейных электрических цепях.

Если магнитные сопротивления магнитной цепи зависят от напряжённости магнитного поля, то такая цепь оказывается нелинейной. Посмотрим, как проводится расчёт в случае нелинейных магнитных цепей.

10.3. Характеристики намагничивания ферромагнетиков

Магнитная индукция в ферромагнитных веществах может иметь при одном и том же значении напряжённости тока различные значения, зависящие от предыдущих состояний материала.

Рассмотрим процесс намагничивания ферромагнитного вещества. Предположим, что вещество первоначально было полностью размагничено, т.е. результирующее поле элементарных токов было равно нулю.

При увеличении напряжённости внешнего поля индукция растёт сначала быстро вследствие того, что элементы тока ориентируются так, чтобы их магнитное поле совпало с внешним магнитным полем (рис. 10.10). При больших значениях индукции (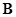) скорость её увеличения уменьшится. Магнитное состояние вещества приблизится к насыщению. При этом уже почти все элементарные токи ориентированы так, что их поля совпадают с внешним магнитным полем. Кривая OD ₁, получающаяся при предварительно полном размагничивании вещества, называется начальной кривой намагничивания. Предположим, что H доведена до Н_m (точка D ₁), а затем уменьшается. При этом кривая B=f (H)располагается выше начальной кривой намагничивания. При Н= 0наблюдается остаточная намагниченность и соответствующая ей остаточная индукция (элементарные токи в известной мере сохраняют упорядоченную ориентацию). Чтобы В= 0, напряженность магнитного поля (Н) должна принять отрицательное значение, называемое коэрцитивной силой (в переводе с латинского языка – удерживающая сила). Если довести Н до отрицательного значения (- Н_m), то индукция примет отрицательное значение, соответствующее точке C ₁. Вновь увеличивая Н до +Н_m,получим ветвь C ₁ D ₂. Повторному уменьшению Н соответствует кривая D ₂ C ₂ и т.д.

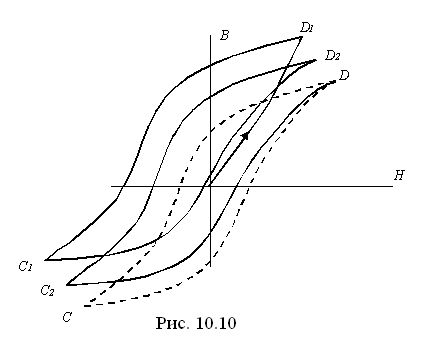
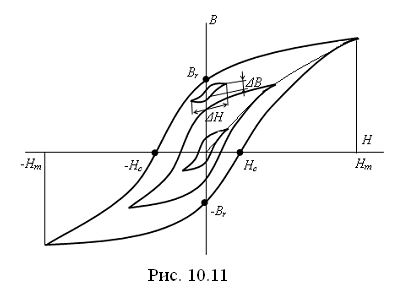
Таким образом, значение индукции при заданном значении H зависит от истории намагничивания. Это явление называется явлением магнитного гистерезиса. Только после достаточного числа (~10) перемагничиваний ферромагнитного материала получаем симметричную гистерезисную кривую CD (пунктирная линия). На рис. 10.11 показано семейство симметричных гистерезисных петель, полученных при различных значениях H_m. Кривая B=f (H), проходящая через вершины симметричных гистерезисных петель, называется основной кривой намагничивания и является вполне определённой для данного сорта материала. Поэтому магнитную проницаемость ферромагнитных материалов принято определять из основной кривой намагничивания. Точно так же остаточная индукция 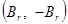и коэрцитивная сила 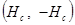определяются из симметричной гистерезисной петли, причём H_m должно быть достаточно велика, чтобы магнитное состояние вещества было близко к состоянию магнитного насыщения. Часть петли, лежащей во втором квадрате и ограниченной изменением индукции от +B_r и Н= 0 до В= 0 и H=H_c, называют кривой размагничивания. Гистерезисная петля, одна из вершин которой лежит на кривой размагничивания, называется частным гистерезисным циклом или частной гистерезисной петлёй.

10. 4. Расчёт нелинейных магнитных цепей

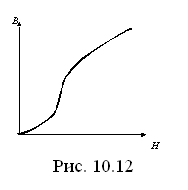Магнитные цепи в технических устройствах содержат участки из ферромагнитных материалов. Как показано на рис. 10.12 процесс намагничивания ферромагнитных материалов имеет специфический вид.

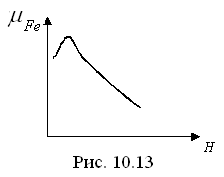Так как 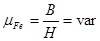(рис. 10.13), то нелинейное сопротивление не остаётся постоянным, заметно увеличиваясь в области насыщения. Поэтому магнитные цепи, содержащие ферромагнитные участки, при относительно сильных магнитных полях следует рассматривать как нелинейные. Методы расчёта таких цепей при пренебрежении потоками рассеяния аналогичны методам расчёта нелинейных электрических цепей.

А. Графический метод

1) Рассмотрим магнитную цепь, показанную на рис. 10.14.

Электрический аналог приведен на рис. 10.15.

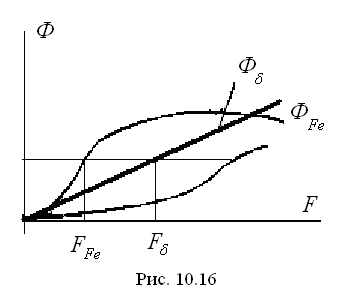
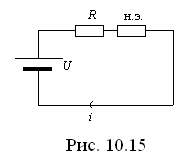Пользуясь характеристикой намагничивания (рис. 10.12), строим кривую зависимости 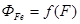. Для этого ординаты кривой 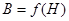умножим на площадь поперечного сечения ферромагнитного сердечника и получим поток Ф_Fe,. Абсциссы умножим на l_Fe и получим МДС F. Используя полученные значения, строим зависимость 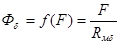(рис. 10.16). Зависимость 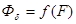для воздушного зазора представляется прямой, т.к. магнитная проницаемость воздуха величина постоянная, равная 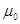. Так как 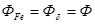, то, складывая абсциссы построенных кривых, получаем , т.е. зависимость магнитного потока от полной МДС .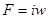

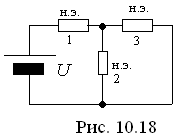
2). Необходимо рассчитать магнитную цепь, показанную на рис. 10.17. Кривая намагничивания ферромагнитного материала представлена на рис. 10.12. Электрический аналог показан на рис. 10.18.

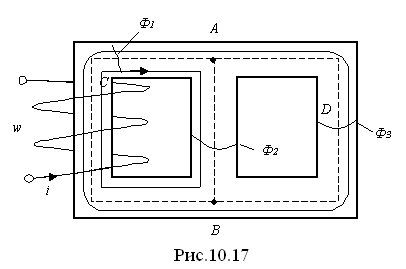
Пользуясь характеристикой намагничивания по аналогии с предыдущим случаем, строим зависимости 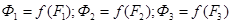(рис. 10.19). Для этого для ряда точек зависимости 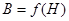умножаем ординату и абсциссу соответственно на S и на l и получаем соответствующие указанной точке значения магнитного потока Ф_i и МДС F_i, что даёт координаты точки i характеристики .

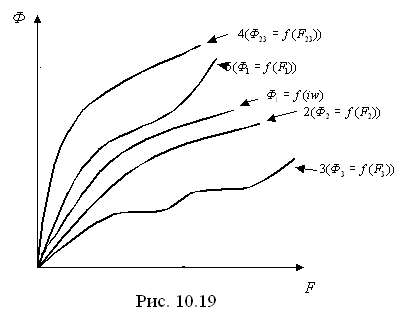
Так как 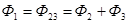и 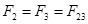, то, складывая ординаты кривых 2 и 3, получим зависимость 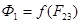(кривая 4). Тем самым 2 и 3 ветви заменяем одной ветвью, включённой последовательно с участком 1. Теперь, складывая абсциссы кривых 4 и 5, получаем кривую 1 (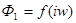), т.к.

.

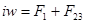Таким образом, получена зависимость магнитного потока в неразветвленной части цепи от полной МДС цепи.

Б. Численные методы

Для расчёта нелинейных магнитных цепей постоянного тока применимы все численные методы расчёта, описанные ранее при рассмотрении нелинейных электрических цепей постоянного тока.

10.5. О расчёте постоянного магнита

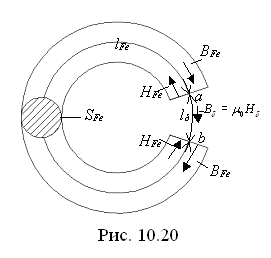Постоянный магнит представляет из себя кольцевой стальной сердечник с воздушным зазором (рис. 10.20). Предположим, что размеры сердечника l_Fe, S_Fe и кривая размагничивания. B (H)для его материала задана. Требуется определить магнитный поток в воздушном зазоре, если сердечник предварительно намагничен до насыщения.

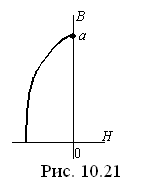
После намагничивания кольцевого сердечника без воздушного зазора магнитная индукция в нём равна B_r, напряжённость поля равна 0.На петле гистерезиса (часть кривой приведена на рис. 10.21) такое состояние соответствует верхней точке кривой размагничивания (точка а).

При наличии воздушного зазора напряжённость поля в сердечнике не равна 0. В самом деле, по закону полного тока имеем

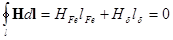. (10.1)

Если l_δ<<l_Fe, то можно считать S_δ=S_Fe. Поэтому

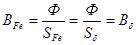
и из уравнения (10.1) следует

,

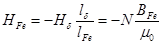где - коэффициент размагничивания.

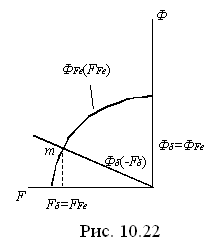Отрицательное значение H_Fe означает, что при наличии зазора начальная индукция снижается по сравнению с 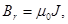это следует из выражения 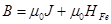. Так как отрицательному значению H_Fe соответствует положительное значение B_Fe=B_δ, то магнитное состояние сердечника определяется одной из точек кривой размагничивания (второй квадрант петли гистерезиса на рис. 10.22)

Построим зависимость 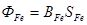от МДС в сердечнике 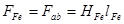. Для этого умножим ординаты точек кривой размагничивания на S_Fe, а абсциссы умножим на l_Fe. Построим далее зависимость Ф_δ от МДС воздушного зазора F_δ.

.

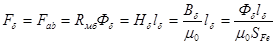Отсюда получаем выражение 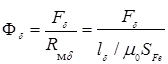, которому соответствует прямая линия.

Так как , то магнитный поток определяется ординатой точки 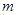, а МДС 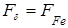абсциссой указанной точки.

Date: 2015-09-17; view: 1412; Нарушение авторских прав