Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
П.1. Классический метод
|
|
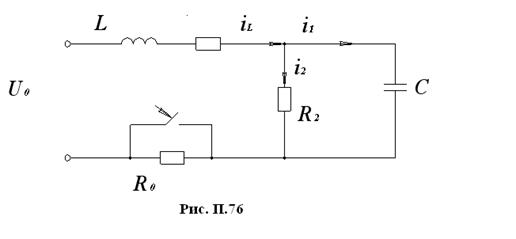
1. Пусть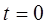 
- момент коммутации.
2. Ток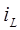 
выбираем в качестве искомой переменной. Этот ток подчиняется законам коммутации.
3. Рассчитаем токи до коммутации, т.е. при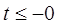 
. Цепь содержит резистор 
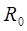. Постоянный ток через конденсатор не проходит, поэтому 
, 
, 
, 
.
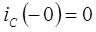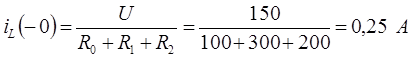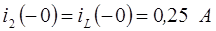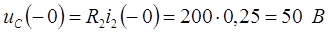4. Используя законы Кирхгофа, запишем уравнения для после коммутационного времени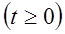 
(П.1)
Приведем данную систему к одному дифференциальному уравнению. В данном уравнении фигурирует только одна переменная - ток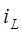 
(или напряжение 
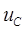), т. к. эти переменные не изменяются в момент коммутации, поэтому при решении дифференциального уравнения в качестве начальных условий можно использовать их значения, которые они принимают до коммутации 
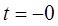. Исключая переменные 
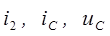, из системы (П.1) получим дифференциальное уравнение второго порядка:
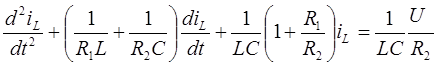. (П.2)
5. Рассчитаем новый установившийся режим цепи (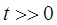
):
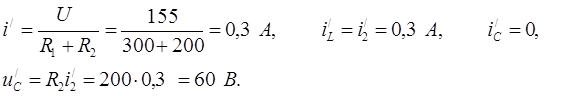
6. Найдем начальные условия: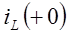 
и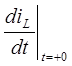 
. Согласно законам коммутации имеем
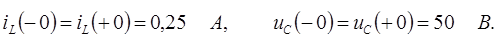
После подстановки этих величин в систему (П.1), записанную для момента времени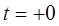 
, получим систему алгебраических уравнений относительно переменных:
.
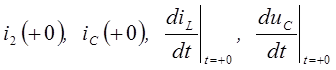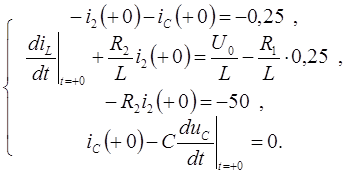
Решая эту систему, определим недостающее начальное условие:
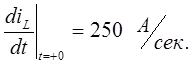
Одновременно найдем: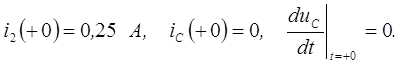 
7. Подставим численные данные в уравнение (П.2) и решим его
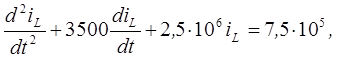(П.3)
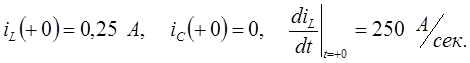(П.4)
Решение неоднородного дифференциального уравнения (П.3) запишем как сумму частного решения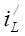 
и общего решения 
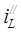однородного уравнения:
. (П.5)
Решение однородного уравнения, называемое свободным током, записывается следующим образом:
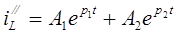. (П.6)
где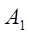 
и 
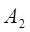- постоянные интегрирования; 
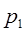и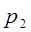 
- корни характеристического уравнения:
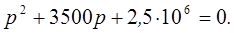
Решаем это уравнение и находим:
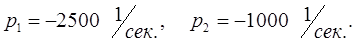
Решение (П.5) запишем следующим образом:
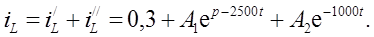(П.7)
Продифференцируем это уравнение:
.
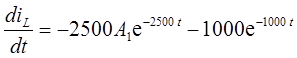8. Вычисли постоянные интегрирования. Используя начальные условия (П.4), запишем систему уравнений для расчета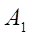 
и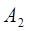 
:
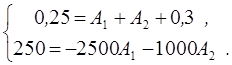
Решая эту систему, найдем: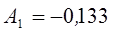 
, 
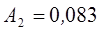. Подставим вычисленные величины в правую часть уравнения, и получим решение
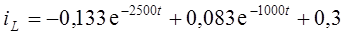A. (П.8)
Расчет остальных токов и построение графиков.
Подставим (П.8) в систему (П.1) и найдем токи:
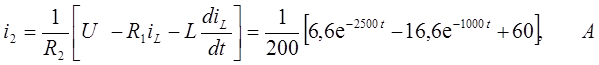
A,
и напряжение на конденсаторе:
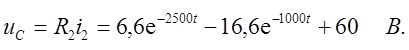
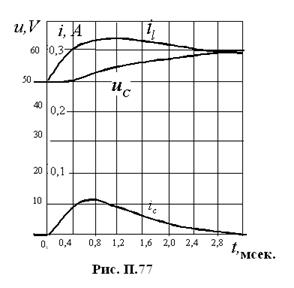
Данные расчетов сведены в табл. П.6. На рис. П.77 приведены соответствующие графики на временном интервале:
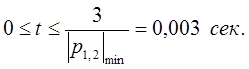
Таблица П.6
| № | t | iL (t) | i2 (t) | iC (t) | uC (t) |
| cек. | A | A | A | В | |
| +0 | 0,260 | 0,250 | 50,0 | ||
| 0,4×10-3 | 0,307 | 0,256 | 0,050 | 51,3 | |
| 0,8×10-3 | 0,319 | 0,267 | 0,052 | 53,2 | |
| . . . | . . . | . . . | . . . | . . . | . . . |
| 3,0×10-3 | 0,304 | 0,296 | 0,008 | 59,2 |
Задачу можно было решить, не решая дифференциального уравнения (П.3). Общее решение для тока может быть сразу представлено в виде:
.
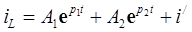Дифференциальное уравнение не решается. Корни характеристического уравнения определяются, используя матрицу контурных сопротивлений:
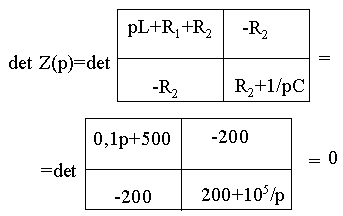
или матрицу узловых проводимостей (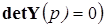
). Источник напряжения закорочен.
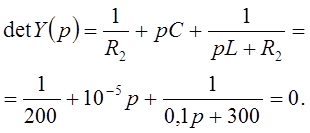
Оба уравнения дают одно и тоже решение:
, 
.
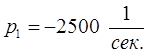Затем можно записать
.
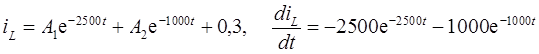Дальнейшее решение совпадает с рассмотренным ранее.
Date: 2015-09-17; view: 407; Нарушение авторских прав