V. Особенности расчета переходных процессов в цепях с емкостными контурами и индуктивными сечениями

Контуры, состоящие только из емкостей или емкостей и источников ЭДС, называются емкостными контурами.

Сечения, состоящие только из индуктивностей или индуктивностей и источников тока, называют индуктивными сечениями.

Если в цепи в результате коммутации образуются емкостные контуры или индуктивные сечения или те и другие, то законы коммутации применимы только к емкостям и индуктивностям, не входящим в указанные контуры и сечения. Для емкостей емкостных контуров применяется закон неизменности заряда, а для индуктивностей индуктивных сечений применяется закон неизменности потокосцепления. Рассмотрим эти законы.

Закон неизменности заряда формулируется следующим образом: алгебраическая сумма зарядов емкостей, присоединенных к любому общему узлу, неизменна в момент коммутации. Т.е. 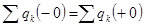, отсюда

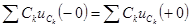. (5.1)

Сумму зарядов записывают с учетом положительных направлений напряжений на емкостях аналогично I закону Кирхгофа для токов, при этом учитывают только емкости емкостных контуров.

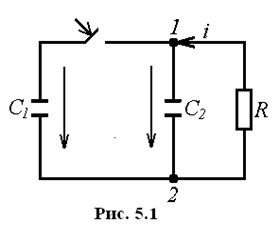
Пример (рис. 5.1).

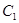Полагаем, что предварительно заряжен до напряжения 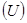, т.е. 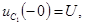а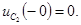

В емкостном контуре имеем два узла 1 и 2. Для любого из этих узлов закон (5.1) принимает вид:

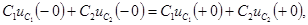но 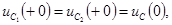поэтому

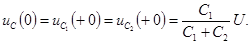
После коммутации цепь описывается уравнением 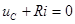, но 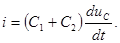Учитывая это, получим 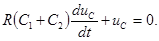Решение этого уравнения записывается следующим образом 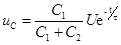, где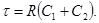

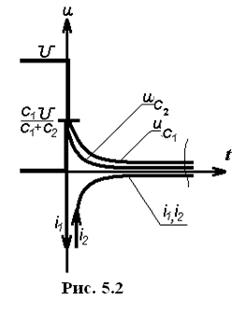
Скачкообразное изменение напряжений обусловлено импульсными токами емкостей, которые возникают в момент коммутации и осуществляют мгновенное перераспределение зарядов между емкостями (рис. 5.2).

Закон неизменности потокосцепления формулируется так: алгебраическая сумма потокосцеплений индуктивностей в любом замкнутом контуре не изменяется во время коммутации, т.е.

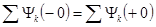или .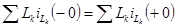

Сумму 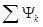записывают с учетом положительных направлений токов в индуктивностях и направления обхода контура аналогично II закону Кирхгофа для напряжений, при этом учитываются только индуктивности индуктивных сечений.

Пример.

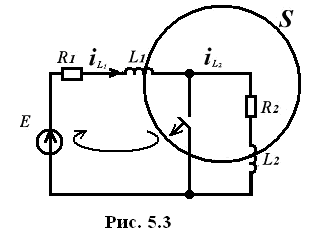
После коммутации цепи (рис. 5.3) имеем один контур, в который входят обе индуктивности сечения s.

Можно записать 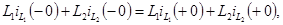где

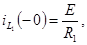
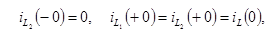
поэтому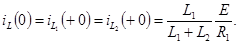

После коммутации цепь описывается уравнением:

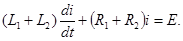
Решение этого уравнения следующе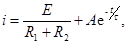е: где .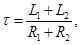

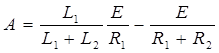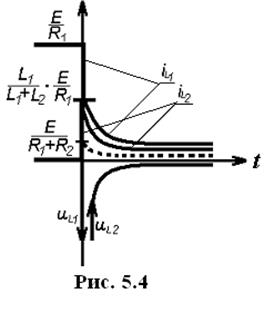Переходной ток равен: .

В момент коммутации 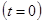токи изменяются скачком (рис. 5.4), т.к. на индуктивностях возникают импульсные напряжения, приводящие к мгновенным перераспределениям магнитного потока между катушками.

Пример

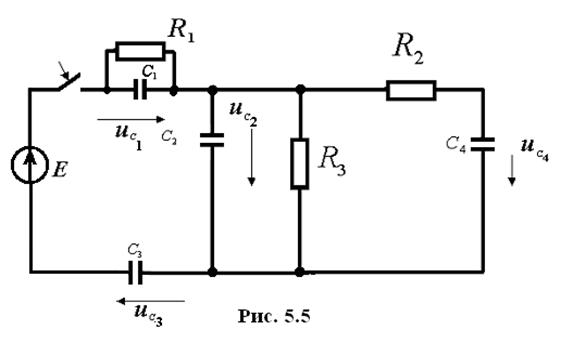
Необходимо составить уравнения для определения начальных значений напряжений на емкостях схемы (рис. 5.5).

После замыкания ключа в схеме образуется емкостной контур 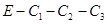. Для узлов 1 и 2 составим уравнения неизменности заряда:

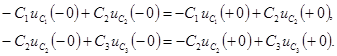
По II закону Кирхгофа для емкостного контура получим уравнение:

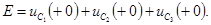
Из этих уравнений определим 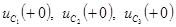при известных значениях .

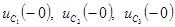Емкость 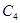не входит в емкостной контур, поэтому ее напряжение непрерывно: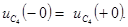

Пример

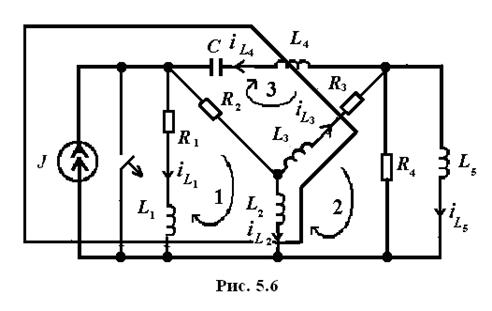
Составить уравнения для определения начальных значений токов в индуктивностях схемы (рис. 5.6).

При отключении ключа в схеме образуется индуктивное сечение .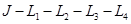

Для указанных на рис. 5.6 трех контуров составим уравнения неизменности потокосцеплений:

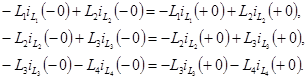
По I закону Кирхгофа для сечения получим уравнение:

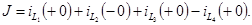
Из этих уравнений находим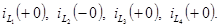

Индуктивность 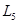в сечение не входит, поэтому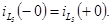

Заключение

Рассмотрим достоинства и недостатки расчета переходных процессов рассмотренными методами.

В цепях с характеристическим уравнением первой или второй степени трудности расчета небольшие и примерно одинаковы, каким бы методом ни производили расчет. Классический метод в этих случаях даже несколько проще. Чем выше степень характеристического уравнения, тем больше уравнений нужно решать совместно при определении постоянных интегрирования и тем больше возрастают трудности расчета при пользовании классическим методом. Для разветвленной цепи с характеристическим уравнением выше четвертой или пятой степени расчет классическим методом представляет известные трудности из-за сложности определения четырех и более постоянных интегрирования.

Если цепь представляет собой полный многоугольник, т.е. каждый узел связан ветвью со всеми остальными узлами, то трудности определения постоянных интегрирования, свойственные классическому методу, возрастают с увеличением числа узлов и степени характеристического уравнения. В более простых цепях, когда все узлы не связаны друг с другом, часто можно значительно уменьшить число уравнений, которые нужно решать совместно. В особенности это касается цепей с двумя узлами. В последнем случае, как и в ряде других, разумно ввести в рассмотрение потенциалы узлов.

Таким образом, если степень характеристического уравнения выше четвертой – пятой, классическим методом пользоваться менее целесообразно, а нужно пользоваться операторным методом.

Переходя к операторному методу, сравним два варианта – расчет переходных токов по теореме разложения и расчет свободных токов по их изображениям.

При расчете операторным методом не нужно определять постоянные интегрирования из начальных условий решением какой-либо системы уравнений. Кроме того, при расчете изображений в эквивалентных операторных схемах можно пользоваться всеми ранее известными методами расчета цепей при установившихся режимах. Эти два момента и определяют достоинства операторного метода.

К недостаткам операторного метода надо отнести утомительность вычисления слагаемых сумм в теореме разложения. Если при расчете по теореме разложения находятся сразу переходные токи, то из-за наличия внешних ЭДС (гармонических с разными частотами и экспоненциальных с разными коэффициентами затухания) усложняются многочлены в составе изображения какого-либо тока или напряжения. Если, например, цепь содержит три гармонические ЭДС разной частоты, то число слагаемых в теореме разложения больше степени характеристического уравнения по крайней мере на три. Кроме того, все изображения усложняются за счет внутренних (расчетных) ЭДС 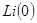и . 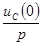Отметим также, что обычная форма теоремы разложения неприменима при наличии кратных корней.

Отметим, что расчет по теореме разложения возможен и для всех таких внешних ЭДС, изображения которых являются отношением двух целых трансцендентных функций.

Расчет операторным методом только свободных токов по их изображениям целесообразен тогда, когда действует ряд различных по характеру внешних ЭДС (гармонических с разными частотами и экспоненциальных с разными коэффициентами затухания). В эквивалентную операторную схему для свободных токов внешние ЭДС не входят, что существенно упрощает изображения токов и напряжений. Однако для определения внутренних (расчетных) ЭДС необходимо рассчитать режим до коммутации и режим после коммутации. Поэтому рассматриваемый вариант операторного метода применим в тех случаях, когда внешние ЭДС имеют простую форму изменения (гармоническую, экспоненциальную, постоянную) и вынужденные токи сравнительно легко найти.

Расчет переходных процессов частотным методом очень близок к расчету операторным методом и характеризуется теми же достоинствами и недостатками. Частотный метод целесообразно применять для расчета переходных процессов в заданной системе в том случае, если для исследования каких-либо других процессов в ней уже применялись частотные методы, аналитическим аппаратом которых является преобразования Фурье. К таким системам относятся, например, линейные системы автоматического регулирования, для которых необходимо исследовать устойчивость при помощи одного из геометрических критериев, исследовать качество регулирования и полностью рассчитать какие-нибудь переходные процессы. Этот метод целесообразно применять при приближенном расчете переходных процессов по вещественной частотной характеристике, особенно когда амплитудная и фазовая частотные характеристики входного сопротивления или проводимости получены экспериментально. В этих случаях метод интеграла Фурье имеет преимущества перед операторным методом. Заметим, что пользуясь операторным методом, входные или взаимные операторные проводимости можно только рассчитать и нельзя получить опытным путем. Проводя же расчет методом интеграла Фурье, получив экспериментально характеристики входных или взаимных проводимостей, имея ЭДС и найдя ее частотный спектр, можно графически найти частотный спектр тока и построить его вещественную или мнимую частотные характеристики. Далее, применяя метод трапеций, можно приближенно рассчитать переходный процесс.

Если напряжение на зажимах пассивного двухполюсника дано кусочно-аналитической кривой, имеющей разрывы, расчет целесообразно вести при помощи интеграла Дюамеля. При этом переходная проводимость или переходная функция находятся одним из известных методов.

Отметим также, что при использовании любым из указанных методов можно задачу расчета переходных процессов с ненулевыми начальными условиями свести к задаче с нулевыми начальными условиями. целесообразность этого приема нужно выяснить в каждом конкретном случае с точки зрения максимально возможного упрощения расчета.

В заключении укажем, что операторный метод и метод интеграла Фурье весьма широко применяются в теории автоматического регулирования и при расчете переходных процессов в электрических машинах, а операторный метод и в некоторой мере метод интеграла Фурье – еще при расчете переходных процессов в цепях с распределенными параметрами, в то время как классический метод во всех этих случаях почти не находит применения.

Date: 2015-09-17; view: 1745; Нарушение авторских прав