
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Преобразование схем при исключении узлов
|
|
Если решать систему узловых уравнений для схемы 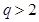 путем исключения неизвестных, то на каждом этапе решения исключение потенциала узла соответствует исключению одного узла схемы.
путем исключения неизвестных, то на каждом этапе решения исключение потенциала узла соответствует исключению одного узла схемы.
Пусть матричное узловое уравнение (2.16) записано в виде
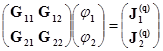 , (2.49)
, (2.49)
где 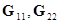 - квадратные неособенные подматрицы (
- квадратные неособенные подматрицы (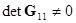 ,
, 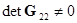 ). Уравнение (2.49) соответствует разбиению матрицы коэффициентов уравнений на блоки.
). Уравнение (2.49) соответствует разбиению матрицы коэффициентов уравнений на блоки.
Так как 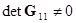 то из (2.49) следует
то из (2.49) следует
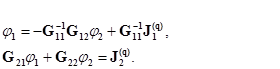 (2.50)
(2.50)
Величину 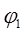 подставим во второе уравнение
подставим во второе уравнение
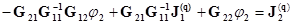 ,
,
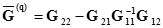 . (2.51)
. (2.51)
Давайте обозначим
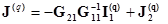 . (2.52)
. (2.52)
Тогда имеем
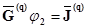 . (2.53)
. (2.53)
Соотношение (2.53) можно считать матричным узловым уравнением схемы, полученной путем исключения узлов, потенциалы которых составляют матрицу 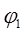
Если 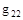 - неособенная квадратная матрица, то можно записать
- неособенная квадратная матрица, то можно записать
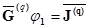 , (2.54)
, (2.54)
где
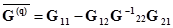 , (2.55)
, (2.55)
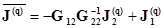 (2.56)
(2.56)
Уравнение (2.54) соответствует матричным узловым уравнениям схемы, полученной путем исключения узлов, потенциалы которых составляют матрицу 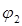 .
.
Схемы, соответствующие выражениям (2.53) или (2.54) может быть получены с помощью выражений (2.51) или (2.55). Эти схемы эквивалентны исходной схеме в том смысле, что имеют одинаковые с ней потенциалы узлов, составляющие матрицу 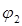 или матрицу
или матрицу 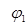 .
.
Матрица 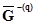 эквивалентной схемы, как видно из (2.51) и (2.55), не зависит от параметров активных элементов (матрицы
эквивалентной схемы, как видно из (2.51) и (2.55), не зависит от параметров активных элементов (матрицы 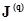 ). Преобразования активных цепей отличаются от преобразований пассивных цепей дополнительной операцией преобразования активных элементов по выражениям (2.52) или (2.56).
). Преобразования активных цепей отличаются от преобразований пассивных цепей дополнительной операцией преобразования активных элементов по выражениям (2.52) или (2.56).
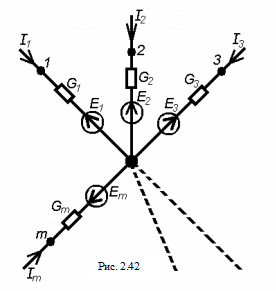 Последовательное исключение узлов схемы может быть выполнено путем многократного применения преобразования звезды в треугольник. На рис. 2.42 дана схема m -лучевой активной звезды.
Последовательное исключение узлов схемы может быть выполнено путем многократного применения преобразования звезды в треугольник. На рис. 2.42 дана схема m -лучевой активной звезды.
Для схемы на рис. 2.42 справедливо уравнение
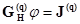 ,
,
где 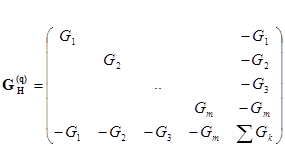
-неопределенная матрица узловых проводимостей, 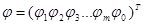 - матрица узловых потенциалов всех узлов,
- матрица узловых потенциалов всех узлов, 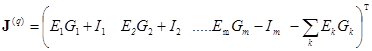 - матрица узловых токов.
- матрица узловых токов.
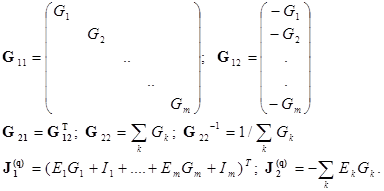 |
Пусть необходимо исключить узел 0 в схеме звезда.
Тогда
 В соответствии с (2.55) имеем
В соответствии с (2.55) имеем
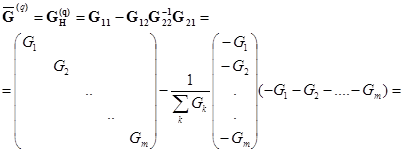
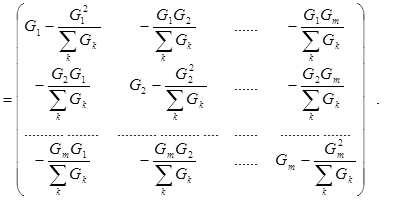 (2.57)
(2.57)
В соответствии с (2.56) имеем
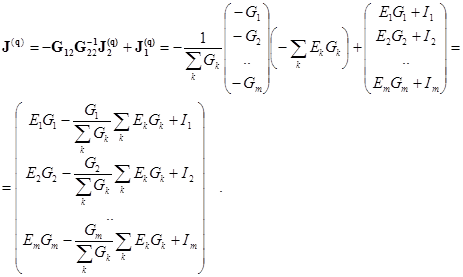 (2.58)
(2.58)
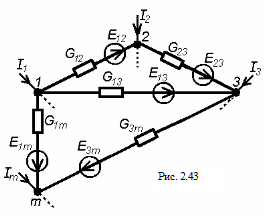 По матрицам (2.57) и (2.58) можно построить схему, эквивалентную звезде. Эта схема имеет вид многоугольника (рис. 2.43). Проводимость ветви
По матрицам (2.57) и (2.58) можно построить схему, эквивалентную звезде. Эта схема имеет вид многоугольника (рис. 2.43). Проводимость ветви 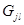 , соединяющей узлы j, l многоугольника, равна элементу (j, l) матрицы (2.57), взятого с противоположным знаком
, соединяющей узлы j, l многоугольника, равна элементу (j, l) матрицы (2.57), взятого с противоположным знаком
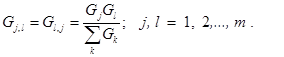 (2.59)
(2.59)
Собственная проводимость каждого узла многоугольника равна соответствующему диагональному элементу матрицы (2.57).
Пассивные параметры 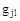 эквивалентного многоугольника определяются однозначно. Активные параметры (ЭДС ветвей) полного многоугольника не может быть найдены единственным образом, т.к. число строк полного многоугольника m (m -1)/2 больше числа независимых элементов матрицы узловых токов (2.58). Эта матрица имеет (m -1) независимых элементов.
эквивалентного многоугольника определяются однозначно. Активные параметры (ЭДС ветвей) полного многоугольника не может быть найдены единственным образом, т.к. число строк полного многоугольника m (m -1)/2 больше числа независимых элементов матрицы узловых токов (2.58). Эта матрица имеет (m -1) независимых элементов.
Чтобы активный многоугольник с проводимостями ветвей (2.57) был эквивалентен активной звезде, достаточно включить по одному соответствующему источнику ЭДС в любую из m -1 ветвей. Если в качестве этих ветвей выбрать ветви, исходящие из узла j, то ЭДС определяются на основании равенства (2.58)
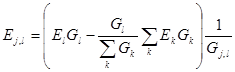 .
.
Беря во внимание (2.59) получаем следующее выражение
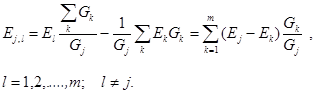 (2.60)
(2.60)
Аналогично решается задача преобразования звезды, ветви которой содержат источники тока. В этом случае источник тока заменяется эквивалентным источником ЭДС.
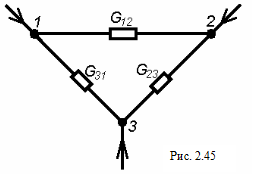
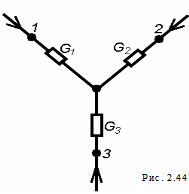 Если звезда пассивна, то формула (2.59) для проводимостей ветвей эквивалентного многоугольника остается справедливой. В случае трех лучевой звезды (рис. 2.44) и эквивалентного треугольника (рис. 2.45) проводимости определяются соотношениями
Если звезда пассивна, то формула (2.59) для проводимостей ветвей эквивалентного многоугольника остается справедливой. В случае трех лучевой звезды (рис. 2.44) и эквивалентного треугольника (рис. 2.45) проводимости определяются соотношениями
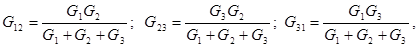 (2.61)
(2.61)
или
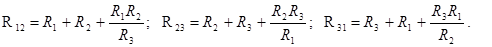 (2.62)
(2.62)
С помощью соотношений (2.50) - (2.55) можно последовательно исключать по одному узлу или сразу группу узлов.
2.12. Преобразование схем при исключении контуров
Матричное контурное уравнение (2.21) запишем в виде
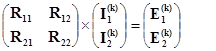 . (2.63)
. (2.63)
Отсюда получаем
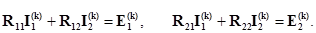
Пусть 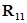 - неособенная квадратная матрица. Тогда
- неособенная квадратная матрица. Тогда
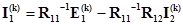 .
.
Данное выражение вносим во второе уравнение
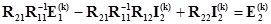 .
.
Обозначим 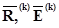 следующим образом
следующим образом
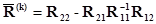 , (2.64)
, (2.64)
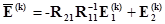 . (2.65)
. (2.65)
Тогда получим
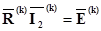 . (2.66)
. (2.66)
Пусть 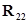 - неособенная квадратная матрица. Тогда
- неособенная квадратная матрица. Тогда
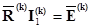 , (2.67)
, (2.67)
где
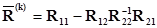 , (2.68)
, (2.68)
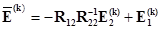 . (2.69)
. (2.69)
Уравнения (2.66) и (2.67) – контурные уравнения эквивалентных схем, полученных исключением контуров. Токи в этих контурах образуют матрицу 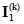 или матрицу
или матрицу 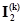 . Эквивалентные схемы имеют контурные токи, совпадающие с токами матриц
. Эквивалентные схемы имеют контурные токи, совпадающие с токами матриц 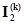 или
или 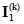 .
.
Пусть схема имеет k независимых контуров и k -й контур исключается. Тогда матрицу контурных сопротивлений 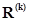 исходной схемы делят на блоки следующим образом:
исходной схемы делят на блоки следующим образом:
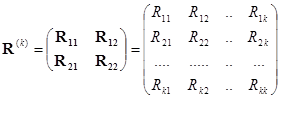 ,
,
где 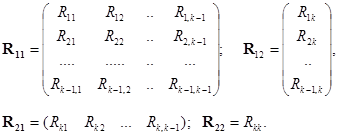
Матрицу контурных сопротивлений схемы с исключенным контуром вычислим по (2.68) при 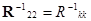
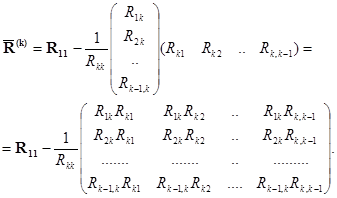 (2.70)
(2.70)
Отсюда получаем собственные сопротивления j -го контура (j =1, 2,.., k -1)
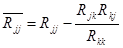 .
.
Общее сопротивление i -го и j -го контуров (j =1, 2,…, k -1) равно
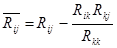 .
.
Если i -й и j -й контуры не имеют общих сопротивлений с исключенным контуром 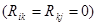 , то собственные сопротивления
, то собственные сопротивления 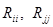 и общее сопротивления
и общее сопротивления 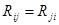 при исключении k -ого контура не изменяются.
при исключении k -ого контура не изменяются.
Матрицу контурных ЭДС исходной схемы представим в виде 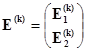 ,
,
где 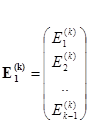 ,
, 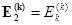 .
.
Согласно (2.69) матрица контурных ЭДС схемы с исключенным контуром равна
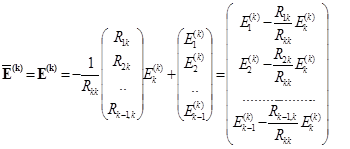 . (2.71)
. (2.71)
Отсюда видно, что при исключении k -ого контура ЭДС j -ого контура равна
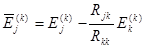 .
.
В общем случае по матрице контурных сопротивлений (2.70) не удается составить эквивалентную схему обычного вида, т.к. при числе контуров больше трех, такая схема не имеет общих сопротивлений для каждой пары контуров.
Для иллюстрации преобразования схемы путем исключения контуров можно ввести условную эквивалентную схему, в которой каждый контур исходной схемы изображается отдельно.
Date: 2015-09-17; view: 652; Нарушение авторских прав