Рачет надежности с учетом старения

В процессе хранения и работы аппаратуры происходят физико-химические изменения свойств материалов из собраны элементы, что в свою очередь вызывает изменения параметров резисторов, емкости С коэффициент усиления транзисторов и ламп, то есть происходит старение и износ элементов. Когда параметры элементов выходят за пределы поля допуска, наступает отказ.

Обычно это параметрические отказы, но они так или иначе нарушают нормальную работу системы. Все элементы имеют определенный срок служб, на этот срок службы влияют многочисленные факторы следовательно результирующий закон изменения времени безотказной работы будет иметь нормальный характер, плотность распределения которого будет иметь следующий вид.

При нормальном законе распределения за время t_ср отказ половины элементов. Для сравнения при экспоненциальном законе за Т_ср отказ 63 % элементов.

Дифференциал нормального закона распределения времени непр. работы записывается.

f(t)=1/σ √2п*exp(-(t –Tcp)²/2σ²); -∞<t<∞

где Т_ср- долговечность элемента или среднее время безотказной работы; σ- среднее квадротическое отклонение σ = √_i=1∑^m(ti–Tcp)²*pi, где m- общие число значений t_i; p_{i -}вероятность того что, что случайное время работы i-го элемента будет равна t_i; Т_ср -определенное значение max по оси времени, а значение σ определяет высоту кривой.

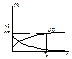Если σ₁>σ_2,то f₁(t)>f₂(t) f(t)=(1/T_o)*e^-t/To=λe^-λt;

₀∫^∞ f(t) dt =1. Эти графики представляют собой плотности времени безотказной работы. Вероятность отказа это площадь под кривой при ₀∫^t.

При нормальном распределении вероятность отказа Qп(t)=₀∫^tf(t)dt=

=(1/σ√2π)₀∫^t exp(-(t–Tcp)² /2σ²)dt

Этот интервал не берущейся, но он табулирован и приведен в справочниках. Так как значение Т_ср для всех элементов разные, то переход к нормирующему. и центрирующему. распределения U=t–T_cp/σ =>σdU = dt.

Тогда: Qп(t)=(1/√2π)₀∫^U exp(-u²/2) du=Ф(U)

Выражение это табулировано и известно под названием функциий Лапласа или Гауссовского интервала ошибок.. Функция Лапласа нечетная Ф(-u)=-Ф(u). Функция симметрична относит. Т_ср Поэтому Ф(0) = 0,5. Ф(u) = Ф0(u) +1/2

Пример: Найти вероятность отказа аппаратуры при следующих параметрах. Т_ср = 10000часов,

σ=3000часов. Найти вероятность отказа системы Qп(t) для 7000, 10000, 13000 часов.

U₁=t-Tcp/σ=7000–10000/3000=-1. U₂ = 10000 – 10000 / 3000 = 0. U₃ = 13000 – 10000 / 3000 = 1

Q_п(7000)=Ф(-1)=-Фо 0,3413(1)+0,5=0,1587; Q_п(10000)=Ф(0)=0+1/2=0,5; Q_п (13000) = Фо(1) +1/2 = 0,8413

Вероятность безотказной работы системы, содержащие N последовательных соединений элементов, по теореме умножения вероятности равна: P_п(t)=_j=1П^N [1–Ф(u)]. Вероятность отказа системы: Qп(t)=1-Pn(t)= _j=1П^N [1–Ф_j(u)]. Если элементы в системе сгруппированы по надежности в к группы число элементов в j- группе то вероятность отказа в такой системе

Р(t)=_j=1П^K [1–Ф_j(u)]^Nj. Тогда можно рассчитать вероятность безотказной работы с учетом внезапных и постепенных отказов

P(t)=Р_в(t) P_n(t)=exp(-t _i=1∑^K λiNi)_i=1П^K [1–Ф_i(u)]^Nj

Частота отказа такого устройства f(t) = f₁(t) P₂(t) + f₂(t) P₁(t)

построим графики этих функций для внезапных отказов Pв(t) и Pп(t) – для износовых. Для десяти равнонадежных элементов No = 10 с инт. отказов

λ1=10*10^-6 1/r среднее время безотказной работы Тср=10000 часов σ = 2000 часов

Для чего нужен расчет с учетом старения, если мы раньше говорили, что аппаратура эксплуатируется до износа. Обычно в любой аппаратуре имеются элементы, которые изнашиваются быстрее других и которые влияют на надежность аппаратуры в целом (например электрические лампы)

эти элементы заменяются и аппаратура работает дольше. При такой замене возникает очень интересный процесс. Рассмотрим его на примере. Возьмем 10000 ламп со среднем временем работы. Тср=7200 часов и σ = 600 часов. График распределения отказов в этом случае будет иметь следующий вид.

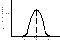99.7% ± 3σ

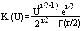За время от 5400 до 9000 часов откажет 9970 ламп следовательно уже приблизительно через 5000 часов лампы будут заменяться новыми и работу будут включатся лампы следующего поколения.Через 7200 откажет половина ламп, а через 14400 часов второй max min отказов, то есть график будет иметь вид

Так как лампы включены в работу не одновременно, то при 2Т_срσ₂>σ₁ и σ₂= σ₁ через t = 3Т_ср, σ₃ =3σ1

В итоге при t= 4Тср число отказов будет постоянно, то есть получаем экспоненциальный закон при 4Тср, но носят только условный характер.

Число отказов становится постоянным при

n=T_cp/3_j,t = nT_cp,где n =7200/1800=4

Интенсивность отказов становится равной λn = 1/T_cp. Для чего нужны эти расчеты. Главным образом для того чтобы выбрать правильные сроки профилактики, для недопущения Износовых отказов. Такие расчеты в редких случаях, так как отсутствует необходимость статистики по срокам службы элементов и их разбросам. Оринтеровачные сроки профилактики можно определить по значению σ, если мы будем проводить профилактику через t=T_cp-3σ, то Q(t)=0,00135; Если через t=T_cp-4σ, то Q(t)=0,000317; Если через t=T_cp-5σ, то Q(t)=0,000000287. Вероятность отказа вроде бы невелика, но если взять систему из большого числа элементов, то профилактики должны производится с интервалом времени не больше, чем через t=T_cp-4σ, и t=T_cp-5σ. Пример Если у самолета менять двигатель через t=T_cp-3σ,

Q(t)=0,00135; Т_ср=1000 часов; σ=200 часов; t_проф=400 часов. Тогда приблизительно на 700 полетов будет приходится 1 отказ. Q(t)=n(Δt)/n; 700=1/0,00135

-------------------------------------------------------------------------------------------------------------------------------------------

Date: 2015-09-05; view: 607; Нарушение авторских прав