Определение параметров нормального закона распределения

Износовые отказы подчиняется нормальному закону распределения и характеризуется двумя параметрами:

Долговечность Т_ср; Среднеквадратичное отношение σ. Такие испытания проводятся для небольших партий элементов, но до отказа всех или почти всех из них. Параметры определяются: Т_ср^*=_i=1∑ⁿ t_i/r

σ ^*= √ _i=1∑ⁿ (t_i-T_cp^*)²/r. Если во время испытаний произошел внезапный отказ, элемент этот из рассмотрения исключаются и не какие даны о нем в последствии не используются. Такие испытания проводятся при нагрузках и внешних условиях, возможно более близких к реальным. В противном случае результаты неточны. Повышение температуры приводит к понижению Т_ср^* и повышению σ^*

-------------------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------------------

47)определение доверительных интервалов при нормальном законе распределения T_ср и большом числе отказов.

Ранее мы получали оценки, которые являются точечными и не являются абсолютно точечными. Истинное значение может быть как меньше так и больше точечных оценок. Поэтому правильнее было бы узнать интервал, в пределах которого заключено истинное значение. Совершенно очевидно, что как бы широк этот интервал не был (в разумных пределах) утверждать со 100 % вероятностью, что истинное значение заключается в нем утверждать нельзя. Можно говорить об этом с той или иной долей вероятности. Например: с вероятность 0,9 можно утверждать, что продолжительность жизни человека находится в интервале между 65 и 75 годами, а с вероятностью 0,99 между 50 и 80 годами. Рассмотрим способы определения доверительных интервалов и критерий доверия, то есть вероятность того, что рассмотренный параметры заключен в указанных параметрах. Если из совокупности N взять несколько выборок. n₁,n₂,…n_k, и для каждой выборки определить Т_ср1,Т_ср2,…Т_срк, то все они будут разными.

Причем отклонения от Т_ср будут распределены нормальным законом. Параметры закона по статистической совокупности определяется по следующим формулам. Т_ср^*= _i=1∑ⁿ t_i/n

S^*=√_i=1∑ⁿ(t_i-T_cp)/n-1, Где S^* несмешанная оценка.

Стандартное отклонение σ=√ _i=1∑ⁿ (t_i-T_cp)² / n. Получаемое значение из ряда выработок опред по след выр: σ (Т_ср) = σ^*/√n, где n- число отказов. Приведенные выражения позволяют непосредственно определить доверительный интервал. Для этого необходимо знать Т_ср и σ.

При числе отказов от 20-30 принять что Т_ср = Т_ср^*, σ = S^*

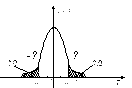
Если мы зададимся доверительной вертикалью, то есть площадью под кривой, то можем определить доверительный интервал. И наоборот, задавшись шириной интервала, можно определить коэффициент доверия.

Установлено, что доверительной интервал будет минимальный, если площадь под кривой плотности распределения U(t) в интервале

(-∞;-2σ(-kα/2)][2σ(kα/2);+∞) будет равны. И если обозначить максимальное отклонение через Е то ширина интервала будет равна Т_ср±ε, а критерий доверия

Р{Т_ср^*–ε≤Т_ср≤Т_ср^*+ε}=1-α. Вычисления критерия доверия, то есть вероятность взятой по обычной методике(по таблице интервала вероятности или функции Лапласа)

γ=1- α =Ф[ε/ σ (Т_ср)] =Ф[(ε √n)/S^*] =2Ф_о(Z), Ф_о–нормированное, центрированное значение. Данная задача может решаться в двух вариантах: 1)опред по заданному критерию доверительных интервалов;2) по заданным доверительным интервалам вычисл критерий доверия

Для 1) Е=Z*S^*/√n;Z=(E√n)/s^*

Пример В результате приведенных испытаний мы получили время безотказной работы t_i для 16 комплектов аппаратуры. Т_ср=_i=1∑ⁿt_i/n=2000 часов;

S^*=[√_i=1∑ⁿ (t_i–T_cp)²/(n-1)]=340 часов; γ = 0,9 принимаем критерия доверия.

По таблице находим что 2Ф_о(z) =0,9 z=1.64. Зная аргумент функции z определяем доверительный интервал.

ε = 1,64*340/√16 = 140. 1860<T_cp<2140 часов с вероятностью 0,9

Пример Определить коэффициент доверия при заданном интервале. Примем доверительный интервал 50 часов ε = 50часов. по таблице находим Ф_о(0,59) = 0,22. γ = 2Ф_о(0,59)= 0,44. Данный метод может использовать, когда много данных об отказах и отказы постепенные и имеют нормальны закон распределения.

И в случае экспоненциального закона или при малых количествах отказов пользуясь этой методикой нельзя, так как в этом случае Тср≠Т_ср^*, а σ≠S*

-------------------------------------------------------------------------------------------------------------------------------------------

48)Определение доверительных интервалов при нормальном законе распределения T_ср и малом числе отказов.

рассмотрим случаи, когда отказы распределения по нормальному закону, но число данных об отказах мало: в этом случае вводится ещё одна случайная велечена. t=T_cp-T_cp^*/S^*

S^*=[√_i=1∑ⁿ(ti–T_cp^*)²]/n(n-1). Случайная величена t подчиняется закону распределения Стьюдента. Особенность этого закона заключается в том, что он не зависит от σ, Т_ср, а зависит от n. Зададимся доверительным коэффициентом t_α и найдем коэффициент доверия. коэффициент доверия вероятность того что искомое значение будет находится в интервале от [-t_α;t_α] пользуясь распределением Стьюдента можно записать что:

γ=P{-t_α ≤t≤t_α}=_-tα ∫^tα S_n(t)dt=2 ₀∫^tα S_n(t)dt

γ=P{-t_αS^*≤T_cp^*-T_ср≤t_αS^*}=2 ₀∫^tα Sn(t)td; t_α=ε/S^*=T_cp^*-T_cp / S^*

Затем по таблице значений Стьюдента в зависимости от t_α, n можно найти коэффициент доверия γ или наоборот в зависимости от выбранного значения γ найти значение Е доверительного интервала.ε=t_αS^*; В соответствии сданными предыдущего примера.

S^*=√[_i=1∑ⁿ(t_i–T_cp)²/n(n-1)]=85. Примем γ = 0,9. тогда при n = 16 из таблицы распределения Стьюдента t_α=1,75; В соответствии с формулой ε= 1,75 * 85 = 149.

Данный способ может использоваться при любом значении распределения отказов.

-------------------------------------------------------------------------------------------------------------------------------------------

49)Определение доверительных интервалов при экспоненциальном законе распределения T_ср и для плана [N,Б,r]

Рассмотрим определенный доверительный интервал для Т_ср при экспоненциальном законе распределения при плане испытаний [N,Б,r] без замены элементов из математики известно, что величина.

U=2S_б(r)λ=2S_б(r)/T_cp. Из математики известно, что U распределена по закону с 2r степеней свободы. Распределения χ² имеет вид:

S_Б(r)=_i=1∑ⁿt_i+(N-r)t_r. Вероятность того что величина U находится в пределах [ χ²₁;χ²₂] равно площади под кривой плотности распределения f_2r(U) и ограниченная значением χ²₁, χ²₂.

γ=P{ χ²₁ ≤U≤ χ²₂ }=

= _χ21 ∫ ^χ22 f_2r(U)dU= _χ21 ∫^∞ f_2r(U)dU- _χ22 ∫^∞ f_2r(U)dU

Интервал _χ22∫ ^∞ f2r(U)dU–табулирован см в справочниках.

Точка образа зависимости λ_н,λ_в, вычисляется значением χ²₁ и χ²₂ по таблице определения коэффициента доверия. γ→ λ_n,λ_в

Установлено что доверительный интервал будет минимальный если площадь под кривой f_2r(U) в интервалах [0,χ²₁],[χ²₂;∞). Тогда абсцисса χ²₁, χ²₂ соответственно ограничивают площадь 0,5(1+γ); 0,5 (1-γ). Последовательность определения доверительного интервала сводится задавшись коэффициентом доверия γ, определить значения 0.5(1+γ); 0.5 (1-γ) и зная число степеней свободы 2r по таблице χ² ² распределения находим значение χ²₁ и χ²₂. А λ_н,λ_в могут быть найдены из следующих неравенств. χ²₂ (2r)≤2S_Б(r)λ≤ χ²₂ (2r). Заменив ≤ на = можно записать Λ_н= χ²₁ (2r)/2S_Б(r); λ_в= χ²₂ (2r)/2S_Б(r)

Т_ов=1/λ_n; Т_он=1/λ_в наработка на отказ

-------------------------------------------------------------------------------------------------------------------------------------------

-------------------------------------------------------------------------------------------------------------------------------------------

Date: 2015-09-05; view: 593; Нарушение авторских прав