Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Виды уравнения плоскостей
|
|
Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному
вектору.
Пусть плоскость задана точкой M0(x0;y0;z0) и вектором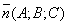 
,
перпендикулярной этой плоскости.
Возьмем произвольную точку M(x;y;z) и составим вектор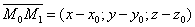 
. При любом расположении точки М на плоскости Q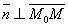 
, поэтому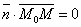 
.
Общее уравнение плоскости.
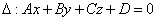
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)
· Если С=0 то вектор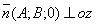 
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то
ox.
· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.
Аналогично при A=D=0 и B=D=0.
· Если А=В=0 то уравнение примет вид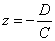 
плоскость параллельна плоскости Oxy.
· Если A=B=D=0, то уравнение имеет вид 
. Это уравнение плоскости Oxy.
Уравнение плоскости, проходящей через три точки
К (х1;у1) М (х2;у2) N (x3;y3)
Возьмем на плоскости точку P (x;y;z).
Составим векторы:
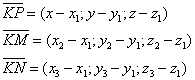
Эти векторы лежат в одной плоскости, следовательно они компланарны:
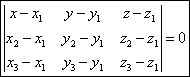
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
; 
; 
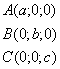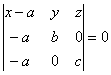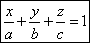
Нормальное уравнение плоскости.
12 Расстояние от точки до плоскости.
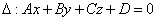
Прямая L: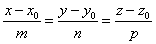 
Пусть φ – угол между плоскостью и прямой.
Тогда θ – угол между 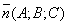и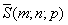 
.
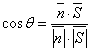
Найдем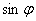 
, если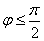 
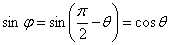, т.к.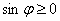 
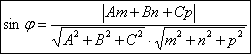
Расстояние от точки до плоскости.
Дано:
M0 (x0;y0;z0)
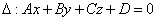
Расстояние d от точки М0 до плоскости ∆ равно модулю проекции
вектора 
(где М
1(x1;y1;z1) - произвольная точка
плоскости) на направление нормального вектора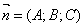 
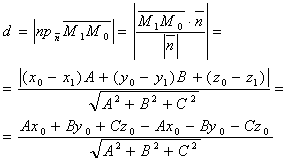
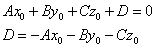
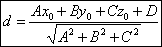
!!!Если плоскость задана уравнением:
то расстояние до плоскости находится по формуле:
функцию сначала прологарифмировать, а результат продифференцировать.
Однако производные степенных функций находят только логарифмическим
дифференцированием.
Производная степенно-показательной функции равна сумме производно
показательной функции, при условии U=const, и производной степенной функции,
при условии V=const.
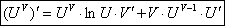
Date: 2015-09-05; view: 505; Нарушение авторских прав