Схема независимых испытаний

Определение: Если при проведении нескольких испытаний вероятность события A в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события A.

Определение: схемой Бернулли называется последовательность n одинаковых независимых испытаний, имеющих 2 возможных несовместных исхода, достигаемых с вероятностями p (успех) и q = 1 - p (неуспех).

Теорема (формула Бернулли): пусть в серии из n испытаний схемы Бернулли событие A произошло в k случаях. Тогда для любого k=0,1,..,n:

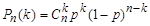, где 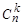-сочетания из n по k, p – вероятность появления события в одном испытании.

Пример 1. Вероятность того, что покупателю потребуется обувь 41-го размера, равна 0,2. Найдите вероятность того, что из 5 первых покупателей обувь этого размера понадобится: а) одному; б) по крайней мере одному; в) менее, чем двум.

а)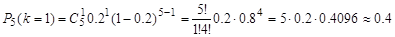

б)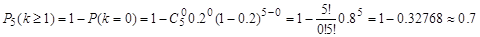

в)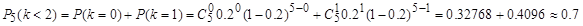

Теорема. В n испытаниях схемы Бернулли с вероятностью успеха p наиболее вероятное число успехов определяется неравенством .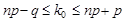

Для нахождения наиболее вероятного числа успехов можно воспользоваться следующим правилом:

a) если число 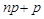не целое, то 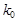равно целой части этого числа ;

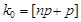б) если число 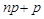целое, то 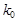имеет два значения 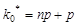и ,.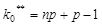

Пример 2. Найти Наиболее вероятное число успехов в схеме Бернулли, где p=0.3, а количество испытаний равно а) n=5; б) n=9.

а) 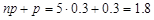- не целое.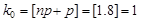

б) 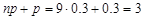- целое. ,

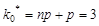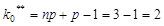
При достаточно больших n использование формулы Бернулли затруднено, так как необходимо вычислять факториалы больших чисел. В этом случае используют формулы для приближенного вычисления вероятности.

Локальная теорема Лапласа. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k) того, что событие A появится в n испытаниях ровно k раз, приближенно равна (тем точнее, чем больше n):

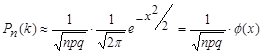при .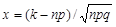

Для получения значения функции 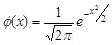используют специальные таблицы, в которых указаны значения этой функции для положительных значений аргумента x. Для отрицательных значений аргумента пользуются теми же таблицами, так как функция 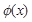четна, то есть .

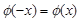Пример 3. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что из 100 новорожденных окажется 50 мальчиков.

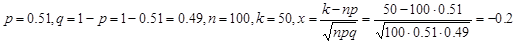
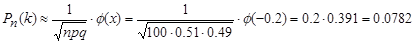
Интегральная теорема Лапласа. Если вероятность p появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁,k₂) того, что событие A появится в n испытаниях не менее k₁ и не более k₂ раз, приближенно равна (тем точнее, чем больше n):

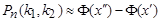
Здесь 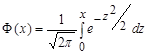-функция Лапласа, ,

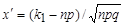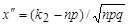
Значения функции Лапласа 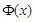определяется по таблицам, в которых приведены значения для положительных аргументов x, не превышающих 5. Если аргумент меньше нуля, то следует учесть, что функция Лапласа нечетная, то есть 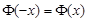. Для аргументов больших 5, значение функции следует принимать равными .

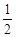Пример 4. Кабельная телекомпания города Бобруйска, решая вопрос о целесообразности покупки прав на трансляцию чемпионата города по мини-футболу, провела опрос среди болельщиков и выяснила, что 20 из 100 болельщиков, не имеющих кабельного телевидения, пожелают по этой причине стать их абонентами. Считая, что в городе Бобруйске 10 000 болельщиков, не охваченных кабельным телевидением, а чистая прибыль от подключения одного абонента составляет 50 бобруйских рублей, выяснить, какова вероятность того, что чистая прибыль компании от привлечения новых клиентов превысит 105 000 бобруйских рублей.

Чтобы получить прибыль более 105 000 б.руб. нужно подключить более 105 000 / 50 = 2 100 новых абонентов. Один абонент подключается с вероятностью p=0.2, тогда q=1-0.2=0.8. Всего может подключиться n=10 000 болельщиков. Таким образом необходимо найти вероятность того, что подключится более 2 100 болельщиков из 10 000.

,

,

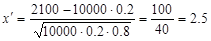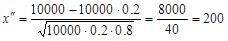
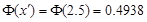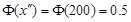
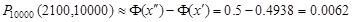
Важным следствием интегральной теоремы Лапласа является формула вероятности того, что в серии из n независимых испытаний отклонение относительной частоты появления события A от его вероятности, не превысит некоторого значения.

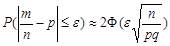, где m-количество испытаний, в которых событие A произошло, n – общее количество испытаний, p – вероятность появления события в одном испытании, q – вероятность того, что событие не появится в одном испытании, e - некоторое число.

Пример 5. Сколько раз надо бросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появления герба от вероятности p=0.5 окажется по абсолютной величине не более 0.01?

e=0.01, p=0.5, q=1-p=1-0.5=0.5

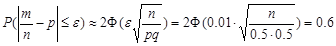
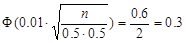
По таблице находим значение x, для которого 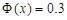: x=0.84.

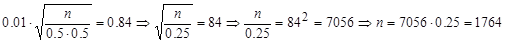
Date: 2015-09-05; view: 10502; Нарушение авторских прав