
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики дискретных случайных величин
|
|
Закон распределения полностью характеризует случайную величину, однако на практике он часто бывает неизвестен. В этом случае используют числа, которые описывают случайную величину суммарно; такие числа называются числовыми характеристика случайной величины.
Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:
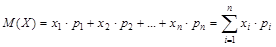
Математическое ожидание есть некоторая постоянная (неслучайная) величина.
Вероятностный смысл математического ожидания: для большого числа испытаний математическое ожидание приблизительно равно среднему арифметическому значению случайной величины.
Пример 1. Найти математическое ожидание дискретной случайной величины X, закон распределения которой приведен ниже:
| X | |||
| P | 0.25 | 0.5 | 0.25 |
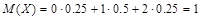
Свойства математического ожидания:
1. Математическое ожидание постоянной величины C равно C:
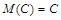
2. Постоянный множитель можно выносить за знак математического ожидания:
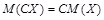
3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:

Две случайные величины называют независимыми, если закон распределения одной из них, не зависит от того, какие значения приняла другая случайная величина.
Пример 2. Пусть ежедневные расходы на обслуживание и рекламу автомобилей в автосалоне составляют в среднем 120 тыс. руб., а число продаж X автомашин в течение дня подчиняется закону распределения:
| X | ||||||||||
| P | 0.25 | 0.2 | 0.1 | 0.1 | 0.1 | 0.1 | 0.5 | 0.5 | 0.025 | 0.025 |
Найти математическое ожидание ежедневной прибыли при цене автомашины в 150 тыс. руб.
Решение. Ежедневная прибыль подсчитывается по формуле: П=150X-120.
M(П)=М(150X-120)=M(150X)-M(120)=150M(X)-120=150×2.675-120=281.25
Математическое ожидание стандартных распределений:
1. биномиального распределения: 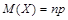 ;
;
2. геометрического распределения: 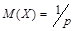 ;
;
3. распределения Пуассона: 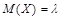 .
.
Определение. Разность между случайной величиной и ее математическим ожиданием называется отклонением: X-M(X).
Теорема. Математическое ожидание отклонения равно нулю: 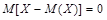 .
.
Определение. Математическое ожидание квадрата отклонения называется дисперсией (или рассеянием):
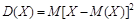
Формула дисперсии в развернутом виде:
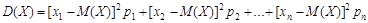
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания: 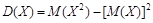
Пример 3. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
| X | |||
| p | 0.1 | 0.6 | 0.3 |
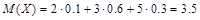
1 способ: 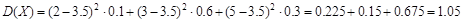
2 способ: 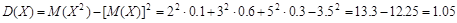
Свойства дисперсии:
1. дисперсия постоянной величины C равна нулю: 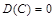 ;
;
2. постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 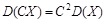 ;
;
3. дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:  ;
;
4. дисперсия разности двух независимых случайных величин равна сумме их дисперсий: 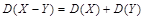 .
.
Дисперсия стандартных распределений:
1. биномиального распределения:  ;
;
2. геометрического распределения: 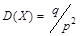 ;
;
3. распределения Пуассона: 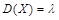 .
.
Определение. Средним квадратическим отклонением (СКО) случайной величины X называется квадратный корень из ее дисперсии 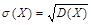
Теорема. СКО суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов СКО этих величин:

Размерность СКО совпадает с размерностью случайной величины.
Пример 4. Банк выдал кредиты n разным заемщикам в размере S ден. ед. каждому под ставку ссудного процента r. Найти математическое ожидание, дисперсию и СКО прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата кредита заемщиком равна p.
Решение: Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем n независимых испытаний. Вероятность утери кредита банка в каждом испытании равна q=1-p. Пусть X – число заемщиков, возвративших кредит с ссудным процентом. Прибыль банка определяется формулой: 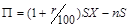 .
.
С.в. X имеет биномиальное распределение, ее математическое ожидание равно 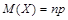 , дисперсия
, дисперсия  .
.
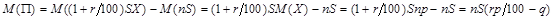
Поскольку выдача кредита имеет смысл лишь при положительной прибыли, то из условия 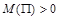 вытекает условие на ставку ссудного процента
вытекает условие на ставку ссудного процента 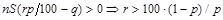 .
.

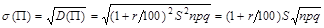 .
.
Начальные и центральные теоретические моменты
Определение. Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk: 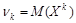
Например, 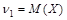 ,
, 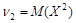 .
.
Определение. Центральным моментом порядка k случайной величины X называют математическое ожидание величины  :
: 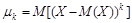
Например, 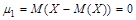 ,
, 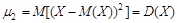 .
.
Date: 2015-09-05; view: 755; Нарушение авторских прав