Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Основные формулы комбинаторики
|
|
Комбинаторика - раздел математики, занимающийся подсчетом числа комбинаций элементов конечного множества, составленных при определенных условиях.
Теорема 1 (правило умножения): пусть каждое из k действий можно выполнить соответственно N1, N2,..., Nk способами, то существует N1N2... Nk способов выполнить все эти действия последовательно.
Теорема 2 (правило сложения): пусть каждое из k действий можно выполнить соответственно N1, N2,..., Nk способами, то существует N1 + N2 +...+ Nk способов выполнить одно из этих действий.
Пример 1: Из пункта A в пункт B ведут 4 дороги. Из пункта B в пункт C ведут 3 дороги. Сколько существует путей из A в C?
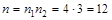
Пример 2: Работы участников олимпиады по математике шифруются либо двумя цифрами, либо буквой латинского алфавита. Сколько различных шифров можно составить?
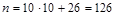
Пример 3: Сколькими способами можно выбрать комиссию из 3 человек (председатель, заместитель секретарь), выбирая ее из 4х супружеских пар, если в комиссию не могут входить члены одной семьи?
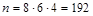
Определение: генеральной совокупностью объема n называется произвольное конечное множество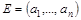 
; выборкой из генеральной совокупности объема k называется произвольный набор элементов E: 
.
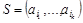Определение: выборка называется упорядоченной, если имеет значение порядок ее элементов, и неупорядоченной в обратном случае. Выборка проводится без повторений, если каждый элемент генеральной совокупности входит в нее не более одного раза, и с повторениями в обратном случае.
Упорядоченные выборки объема k из генеральной совокупности объема n называются размещениями, а неупорядоченные – сочетаниями из n элементов по k.
Подсчет числа выборок объема k из генеральной совокупности объема n:
| Выборки | Упорядоченные (размещения) | Неупорядоченные (сочетания) |
| Без повторений |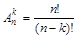 
| 
|
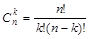
| С повторениями |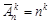 
| 
|
Пример 4: В чемпионате по футболу участвуют 12 команд. Сколькими способами могут быть распределены 1,2 и 3 места.
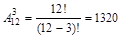
Пример 5:Сколько существует различных способов сдать 6 карт из колоды в 36 карт.
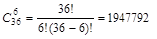
Пример 6: Сколько можно составить различных двоичных чисел, состоящих из трех разрядов?
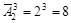
Пример 7:В магазине продается 5 видов открыток. Сколько существует способов выбрать любые 3.
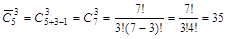
Определение: различные упорядоченные множества, которые отличаются лишь порядком элементов, называются перестановками этого множества. Количество перестановок определяется по формуле: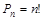 
Различные упорядоченные множества, состоящие из элементов k различных видов, которые отличаются лишь порядком элементов, называются перестановками этого множества с повторениями. Количество перестановок с повторениями определяется по формуле: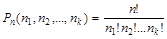 
Пример 8. Сколько различных буквенных сочетаний можно получить, переставляя буквы в слове БАРАБАН?
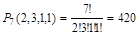
Date: 2015-09-05; view: 1069; Нарушение авторских прав