Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Некоторые сведения из теории множеств
|
|
Случайные события
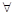- “для любого”, “любой”, 
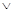- “или”, “хотя бы один”, 
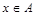- “x принадлежит A”
Определение: Множество - неопределяемое понятие, которое может быть интерпретировано как некоторый набор элементов; пустое множество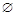 
- множество, не содержащее элементов; 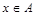обозначает, что элемент x принадлежит множеству A.
Определение: множество B называется подмножеством А(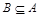
), если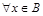 
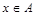; очевидно, что 
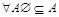. Множества А и В равны, если 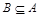и 
.
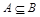Операции над множествами:
1) Объединение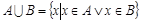 
(Объединение множеств A и B – это множество, состоящее из элементов, принадлежащих хотя бы одному из множеств).
2) Пересечение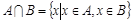 
(Пересечение множеств A и B – это множество, состоящее из элементов, принадлежащих обоим множествам).
3) Разность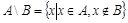 
(Разность множеств A и B – это множество, состоящее из элементов, принадлежащих множеству A и не принадлежащих множеству B).
4) Дополнение - если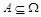 
, то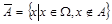 
(Дополнение множества A до множества W - это множество, состоящее из элементов множества W и не принадлежащих множеству A).
Date: 2015-09-05; view: 738; Нарушение авторских прав