Случайные события, их виды

Теория вероятностей занимается установлением закономерностей, которым подчиняются массовые однородные случайные события Теория вероятностей не стремится предсказать единичное событие.

Определение: Однородные события - события, которые происходят при осуществлении одних и тех же условий S и подчиняются определенным закономерностям независимо от природы событий.

Условия S необходимо подробно и тщательно описывать в каждом конкретном случае при постановке задаче исследования случайных событий.

Определение: Событие называется случайным, если в результате испытаний при осуществлении некоторой совокупности условий S оно может произойти или не произойти. Под "испытанием" может пониматься проявление какого-либо природного явления или спланированный исследователем эксперимент над рукотворным или природным объектом.

Определение: Относительная частота - отношение числа появления события A к общему числу испытаний .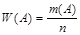

Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях и обладают свойством статистической устойчивости: относительная частота появления события имеет тенденцию стабилизироваться с ростом общего числа экспериментов, приближаясь к некоторому числу P(A).

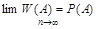
Определение: Элементарный исход - результат одного испытания в определенных условиях.

Элементарные исходы взаимно исключают друг друга, и в результате каждого испытания может произойти только один из элементарных исходов. Обозначение элементарного исхода w_i.

Примеры элементарных исходов:

• результат бросания монеты на идеальную плоскость (w₁=Г, w₂=Р),
• результат бросания игральной кости и выпадение на верхней грани какого- либо числа (w₁=1, w₂=2, w₃=3, w₄=4, w₅=5, w₆=6),
• результат одновременного бросания нескольких монет и выпадение на верхних гранях всех монет определенной комбинации гербов или решек. (Для двух монет: w₁=ГГ, w₂=ГР, w₃=РГ, w₄=РР)

Все элементарные исходы, возможные при определенных условиях, образуют пространство элементарных исходов W: 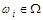, i = 1,2,.... Каждый элементарный исход влечет появление какого-либо события. В общем случае событие A может произойти при появлении элементарных исходов, принадлежащих некоторому подмножеству W_A пространства W, 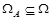(AÎW). Говорят, что событие A произошло, если реализовался любой из входящих в него элементарных исходов. События принято обозначать заглавными латинскими буквами: A, B, C...

Операции над собятиями:

1) Суммой A+B (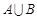) событий A и B называется событие, состоящее в том, что произошло либо A, либо B, либо оба события одновременно. На языке теории множеств 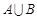есть множество, содержащее как элементарные исходы, входящие в A, так и элементарные исходы, входящие в B.

2) Произведением AB(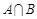) событий A и B называется событие, состоящее в том, что произошли оба события A и B одновременно. То есть 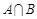есть множество, содержащее элементарные исходы, входящие одновременно в A и в B.

3) Разностью 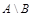событий A и B называется событие, состоящее в том, что произошло событие A, но не произошло B. То есть 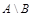есть множество, содержащее элементарные исходы, входящие в A, но не входящие в B.

4) Противоположным (или дополнительным) к событию A называется событие 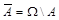, состоящее в том, что событие A в результате эксперимента не произошло. Иначе говоря, A есть множество, содержащее элементарные исходы, не входящие в A.

Виды случайных событий:

· достоверное событие Т - событие которое непременно происходит при появлении любого элементарного исхода в условиях S: T=W

· невозможное событие Æ - событие которое не может произойти ни при одном элементарном исходе из пространства W при условиях S.

· события A и B несовместны, если появление одного из них исключает появление другого из них; о несовместных событиях можно записать: AB=Æ,

· события A и B противоположны, если они несовместны и A+B=W, в этом случае пользуются обозначениям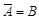и или ,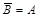

· события A₁,A₂,...,A_n образуют полную группу попарно несовместных событий, если при в результате испытания осуществляется только одно из этих событий и A₁+A₂+...+A_n=W

Date: 2015-09-05; view: 652; Нарушение авторских прав