Условная вероятность. Пример 1. Кубик подбрасывается один раз

Пример 1. Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

В данном случае пространство элементарных исходов состоит из трех равновозможных элементарных исходов: 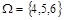, и событию A = {выпало четное число очков} благоприятствуют 2 из них 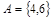. Поэтому P(A) = 2/3.

Вероятность события A, вычисленную в предположении, что нечто о результате эксперимента уже известно (событие B произошло), мы будем обозначать через P(A|B).

Определение. Условной вероятностью события A, при условии, что произошло событие B, называется число .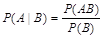

Теорема умножения. Вероятность произведения событий A и B равна P(AB)=P(B)P(A|B)= P(A)P(B|A).

Следствие. Вероятность произведения более чем двух событий, равна

P(A₁A₂...A_n)=P(A₁)P(A₂|A₁)P(A₃|A₁A₂)...P(A_n|A₁A₂... A_n-1).

Пример 2. В группе МГ-21 учится 27 студентов, из них 10 юношей. Декан наудачу выбрал двух студентов для выполнения важной миссии. Найти вероятность того, что было выбрано двое юношей.

1й способ. A₁={первым выбран юноша}, A₂={вторым выбран юноша}.

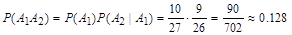
2й способ. Вычислим вероятность по классической схеме.

Вероятность события может быть вычислена по формуле: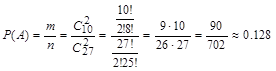

Независимые события

Определение. Событие B называется независимым от события A, если условная вероятность события B равна его безусловной вероятности (появление события A не влияет на вероятность события B):

.

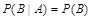Теорема умножения для независимых событий может быть записана в виде:

P(A₁A₂...A_n)=P(A₁) P(A₂)... P(A_n)

Пример 3. Куплено 2 изделия, изготовленных на разных заводах. На первом заводе брак составляет 2%, а на втором – 5%. Найти вероятность того, что оба изделия бракованные.

A₁={первое изделие бракованное}, A₂={второе изделие бракованное}.

P(A₁A₂)= P(A₁) P(A₂)=0.02*0.05=0.001

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий равна P(A+B)=P(A)+P(B).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий равна сумме вероятностей этих событий: P(A₁+A₂+..A_n)=P(A₁)+P(A₂)+...+P(A_n).

Теорема сложения вероятностей совместных событий. Вероятность появления одного из двух совместных событий равна P(A+B)=P(A)+P(B)-P(AB).

Следствие. Для зависимых событий: P(A+B)=P(A)+P(B)-P(A)P(B|A)

Для независимых событий: P(A+B)=P(A)+P(B)-P(A)P(B)

Пример 4. Вероятности поражения цели первым и вторым орудиями равны 0.9 и 0.8. Найти вероятность поражения цели при залпе.

A₁={первое орудие поразило цель}, A₂={второе орудие поразило цель}.

P(A₁+A₂)=P(A₁)+ P(A₂)-P(A₁A₂)= P(A₁)+ P(A₂)-P(A₁)P(A₂)=0.9+0.8-0.72=0.98

Пример 5. Условие примера 3. Найти вероятность того, что только одно изделие бракованное.

A₁={первое изделие бракованное}, A₂={второе изделие бракованное}.

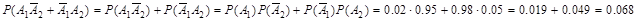Теорема. Вероятность появления хотя бы одного из событий A₁, A₂, …, A_n определяется формулой:

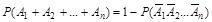
Следствие. Вероятность появления хотя бы одного из независимых событий равна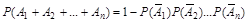

Пример 6. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того что, по крайней мере, один человек из них может квалифицированно оценить продукт?

Вероятность того, что один выбранный наудачу человек является потребителем продукции, равна p=0.1. Тогда

Date: 2015-09-05; view: 2391; Нарушение авторских прав