Теплоемкость твердых тел

В 1907 г. Эйнштейн показал, что формула Планка для средней энергии осциллятора

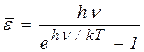
непосредственно подтверждается тепловыми свойствами твердых тел. Из опыта известно, что при высоких температурах справедлив закон, называемый законом Дюлонга и Пти, который утверждает, что теплоемкость одного моля любого твердого вещества составляет примерно 6 кал/град. С классической точки зрения этот закон вполне понятен. В твердом теле каждый атом можно рассматривать как трехмерный гармонический осциллятор, поскольку, согласно нашим представлениям, атом удерживается в определенном положении равновесия некоторой квазиупругой силой. Поэтому по правилам классической статистики ему следует приписать в среднем полную энергию 3kT, так что моль вещества будет обладать энергией U=3 kT = 3RT, где R – универсальная газовая постоянная, равная приблизительно 2 кал/град. Отсюда легко найти теплоемкость как приращение энергии, соответствующее повышению температуры на 1 градус. Итак,

кал/град.

Однако на опыте наблюдаются отклонения от этого правила: чем тверже тело, т.е. чем крепче «привязаны» атомы к положению равновесия, тем заметнее эти отклонения. Так, например, для алмаза теплоемкость одного моля составляет при комнатной температуре всего лишь около 1 кал/град.

Эйнштейн объяснил эти отклонения тем обстоятельством, что в этом случае нельзя пользоваться классическим выражением для средней энергии: необходимо обратиться к формуле Планка для средней энергии квантового осциллятора. Тогда энергия одного моля вещества будет равна

.

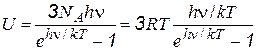В этой формуле h ν есть элементарный квант колебательной энергии осциллятора; он тем больше, чем прочнее удерживается атом в положении равновесия, так что слабая связь эквивалентна малой колебательной энергии, а стало быть, малой частоте. Важный вопрос состоит в том, какая из величин больше: hν или kT. Обычно при комнатных температурах 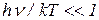, так что формулу для средней энергии можно упростить разложением в ряд, В этом случае она переходит в классическую формулу

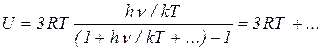
и, таким образом, приводит к закону Дюлонга и Пти.

При больших значениях температуры теплоемкость приближается к классическому пределу 6 кал/грал, а при малых температурах убывает, обращаясь в нуль при T =0. Экспериментальные исследования, имеющие целью проверку предсказаний теории и проведенные в основном Нерстом и его сотрудниками, показали, что имеет место приблизительное согласие между экспериментом и теорией, особенно в связи с тем фактом, что теплоемкость стремится к нулю по мере приближения к нулю температуры. Тем не менее были обнаружены и расхождения, свидетельствующие о том, что теория в той форме, в какой она тогда существовала, нуждалась еще в некоторых уточнениях.

Эти уточнения были сделаны Дебаем и независимо Борном и Карманом (1912 г.). Они основываются на следующих соображениях. До сих пор мы считали, что каждый отдельно взятый атом в твердом теле совершает гармонические колебания совершенно независимо от других атомов. Однако на самом деле это вовсе не так, поскольку атомы кристаллической решетки, вне сомнения, очень сильно связаны друг с другом. Поэтому не следует думать, что атомов кристалла колеблются с одинаковой частотой. Скорее необходимо рассматривать связанную систему 3 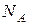различных колебаний (соответственно 3 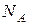степеням свободы 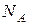атомов, находящихся в одном моле). Энергия системы поэтому будет иметь вид

,

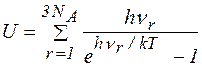где 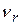– частота r -го колебания.

Непосредственное вычисление этой суммы на основе какой-либо конкретной модели задача довольно не простая. Дебаем была получена приближенная формула для атомов одного сорта. Он рассматривал нормальные колебания атомов кристаллической решетки как колебания кристалла в целом и получил для энергии выражение

,

где 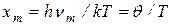, причем 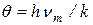называется дебаевской характеристической температурой. 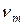– это максимально возможная частота. Эта формула дает более точное приближение к действительности, чем эйнштейновская модель.

Date: 2015-09-05; view: 281; Нарушение авторских прав