Уравнение Шредингера. Стационарные состояния

Для отыскания вида волновой функции необходимо составить уравнение, учитывающее движение микрочастицы и взаимодействие ее с другими частицами вещества. Решением этого уравнения и должна являться волновая функция. Вероятностное истолкование волн де Бройля и соотношений неопределенностей указывают, что уравнение движения в квантовой механике должно быть таким, чтобы оно позволяло объяснять наблюдаемые на опыте волновые свойства частиц. Поскольку состояние частицы в пространстве в данный момент времени как раз и определяется заданием волновой функции Y(x, y, z, t), то основное уравнение квантовой механики должно быть волновым уравнением относительно функции Y(x, y, z, t).

Основное уравнение нерелятивистской квантовой механики было найдено Шредингером (1926 г.). Как и уравнения движения Ньютона, лежащие в основе классической механики и поэтому не выводимые, уравнение Шредингера постулируется. Справедливость уравнения Шредингера доказывается тем, что все выводы, полученные с помощью этого уравнения в атомной и ядерной физике, находятся в хорошем согласии с опытом. Для случая движения частицы в потенциальных силовых полях, характеризуемых потенциальной функцией U, где 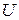– потенциальная энергия (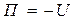), уравнение Шредингера имеет вид

,

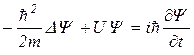где i – мнимая единица (i² = –1),

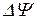– оператор Лапласа («лапласиан»); в прямоугольной декартовой системе координат записывается в виде

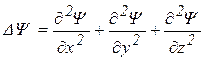. (9.1)

Вид Y- функции для конкретной микрочастицы определяется потенциальной энергией U. Если она не зависит от времени, то Y- функцию можно представить в виде произведения двух сомножителей, один из которых зависит только от координат, а другой – только от времени:

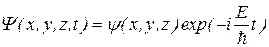, (9.2)

где E – полная энергия частицы.

Подставим полученное выражение для Y -функции в уравнение (9.1):

.

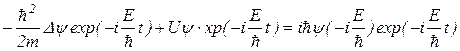После деления уравнения на множитель 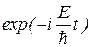, имеем

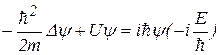, или

.

Полученное соотношение называется уравнением Шредингера для стационарных состояний (поле стационарно, когда его характеристики не зависят от времени). Это уравнение чаще записывают в виде

.

В стационарных состояниях ни одна из квантово-механических вероятностей не изменяется с течением времени. Средние значения всех физических величин также не зависят от времени. В частности, постоянным по времени оказывается среднее значение координаты . Стационарность состояния не исключает зависимость волновой функции от времени, а только ограничивает ее гармоническим законом 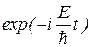. Состояние стационарно, так как равен единице модуль множителя 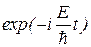, т.е.

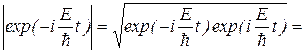1.

Поэтому плотность распределения координат частиц от времени не зависит. В стационарном состоянии плотность вероятности выражается только через (x, y, z). Поэтому y (x, y, z) также называется волновой функцией, хотя, строго говоря, она является только координатной частью всей волновой функции Y (x, y, z, t) стационарного состояния.

Рассмотрим движение частицы вдоль оси x в отсутствие поля. В этом случае потенциальная энергия свободно движущейся частицы U = 0. Согласно гипотезе де Бройля движение такого микрообъекта моделируется монохроматической волной, занимающей все пространство. Поэтому можно предположить, что Y- функция будет иметь следующий вид:

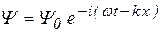, (9.3)

где Y ₀ – амплитуда волны.

Круговая частота w и волновое число k связаны с полной энергий E и импульсом p соотношениями и . Волновая функция (9.3) при этом приобретает вид 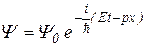. Покажем, что данный вид Y- функции не противоречит уравнению Шредингера. Для этого проделаем следующее:

1. Найдем DY и выразим p ²:

,

.

.

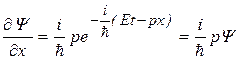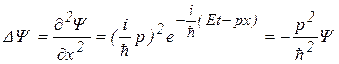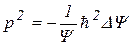2. Найдем и из полученного соотношения выразим полную энергию E:

.

.

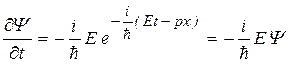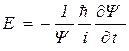3. Воспользуемся соотношением между энергией частицы E и ее импульсом p:

.

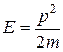В результате получим

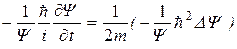
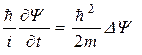или

.

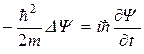Полученное соотношение совпадает с уравнением Шредингера для случая U = 0.

Date: 2015-09-05; view: 298; Нарушение авторских прав