Классическая теория черного излучения

Заметим сначала, что, не выходя за пределы термодинамики и электромагнитной теории света, можно кроме теоремы Кирхгофа вывести еще два закона для черного излучения. Так, закон Стефана (1879 г.) утверждает, что полная энергия излучения пропорциональна четвертой степени температуры 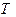излучающего тела. Следующий шаг был сделан Вином (1893 г.), сформулировавшим закон смещения, который носит его имя и утверждает следующее.

Спектральное распределение плотности энергии подчиняется уравнению

,

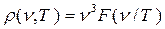где 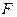– функция, зависящая только от отношения частоты к температуре, конкретный вид которой нельзя установить термодинамическими методами.

Отметим, что закон Вина включает и закон Стефана; чтобы получить его, надо проинтегрировать формулу Вина по всему спектру:

.

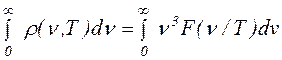Сделав замену переменных 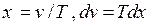, получим

.

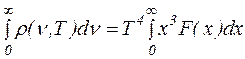Очевидно, что интеграл даст просто число, т.е. действительно, если верен закон Вина, то полная энергия излучения оказывается пропорциональной четвертой степени температуры. Причина, по какой закон Вина называют «законом смещения», такова: экспериментально было обнаружено, что интенсивность излучения раскаленного тела, температура которого поддерживается постоянной, как функция длины волны ведет себя следующим образом (см. рис. 19). При некоторой 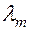наблюдается максимум, который с изменением температуры смещается, в то время как произведение 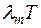оказывается постоянным:

.

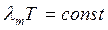Это можно легко доказать, используя закон Вина. Запишем его через : .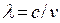

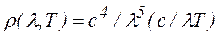Условие максимума функции:

,

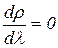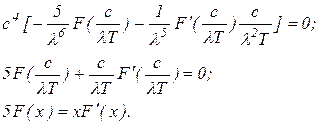
Уравнение содержит всего одну неизвестную величину 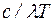, и его решение, если оно существует, должно иметь форму 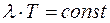. Значение постоянной нельзя определить, если неизвестна функция 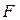. Таким образом и получается теорема о смещении максимума. Чтобы найти 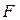, необходимо обратиться к конкретной модели. Исходя из термодинамики ясно, что форма закона, определенного той или иной функцией 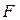, не должна зависеть от конкретного механизма излучения. Поэтому в качестве простейшей модели излучающего тела Планк выбрал линейный гармонический осциллятор с собственной частотой 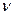. Для такого осциллятора мы можем, с одной стороны, рассчитать энергию, излучаемую за 1 с; (она будет равна просто энергии излучения колеблющегося диполя), и работу, произведенную над осциллятором полем излучения за то же время. В случае равновесия обе эти величины должны совпадать, и при этом получается

,

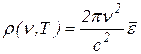где 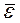– энергия осциллятора, усредненная по некоторому промежутку времени, который велик по сравнению с периодом, но все же настолько мал, что излучением за это время можно пренебречь.

Таким образом, если мы знаем среднюю энергию осциллятора, то мы знаем также и распределение интенсивности черного излучения. Значение 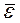, определенное методами классической статистики, оказывается равным 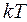. Здесь 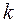– постоянная Больцмана. Это частный случай общего результата статистической механики – закон равнораспределения. В соответствии с этим каждый член в гамильтониане 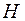(полная энергия), пропорциональный квадрату координаты или импульса, дает один и тот же вклад в среднюю энергию, а именно 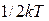, а в гамильтониане осциллятора есть два таких члена и, следовательно, его энергия есть 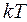. Это можно легко посчитать. По статистике Больцмана, при равновесии состояние осциллятора, характеризуемое энергией 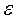, встречается с относительной вероятностью 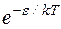, так что 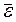получается в результате усреднения по всем состояниям:

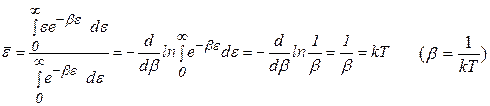Таким образом, получаем

.

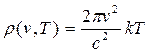Это выражение представляет собой закон излучения Релея – Джинса (1900, 1909 гг.). Заметим, что этот закон согласуется с законом Вина, чего и следовало ожидать. В длинноволновой области, т.е. при малых частотах, закон Релея – Джинса также очень хорошо согласуется с экспериментальной кривой распределения плотности излучения. В этой области плотность возрастает пропорционально второй степени частоты. Но для больших частот формула уже не верна. Из эксперимента известно, что проходя через максимум, плотность излучения ведет себя так, как на рис.19, чего не следует из полученной формулы. Мало того, что отсутствует максимум, так 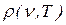непрерывно возрастает как квадрат частоты, что приводит к расходимости интеграла:

.

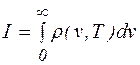В этом случае имеет место «ультрафиолетовая катастрофа».

Предпринимались попытки устранить эту явную несуразицу с помощью следующей гипотезы. Предположим, что для достижения равновесия требуется определенное время (время релаксации). Пусть для черного излучения это время очень велико, т.е. равновесие устанавливается не скоро. Но за это время, как нетрудно представить, свойства системы могут полностью измениться в результате внешних воздействий. Однако эти рассуждения не затрагивают существа дела. Действительно, мы всегда можем, по крайней мере теоретически, как угодно долго поддерживать внешние условия неизменными. Тогда рано или поздно равновесие все же установится.

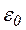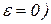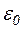В такой ситуации Планк выдвинул смелую гипотезу, что все эти трудности можно обойти, допустив существование конечных дискретных квантов энергии , таких, что энергия осциллятора может оказаться равной (помимо лишь , 2 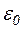, … и т.д. Именно таким образом и выводится закон излучения Планка, который получил блестящее экспериментальное подтверждение. Самое важное – суметь найти среднюю энергию 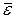. Формально вычисление интегралов заменяется на вычисление сумм. По-прежнему состояние с тем или иным значением энергии встречается с относительной вероятностью, определяемой больцмановским множителем, но теперь в расчетах фигурируют уже не все энергии, как это было раньше, а лишь энергии вида 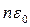( 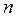=0,1,2, …), поэтому среднее значение энергии равно

.

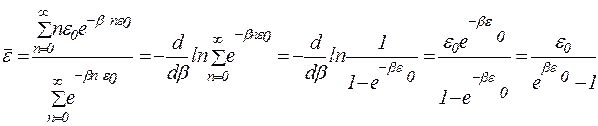Подставляя это выражение в формулу, будем иметь

.

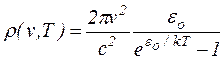Чтобы это выражение не противоречило закону Вина, который, будучи прямым следствием термодинамики, справедлив при всех обстоятельствах, необходимо принять, что

,

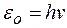где 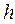– постоянная, носящая имя Планка.

Теперь отсюда прямо следует закон излучения Планка:

.

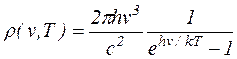Как уже говорилось, эта формула отлично согласуется с опытом.

При малых частотах плотность излучения возрастает приблизительно как квадрат частоты; если 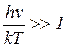, то экспоненту в знаменателе можно разложить в ряд по степеням, причем первый член разложения в точности соответствует закону Релея – Джинса:

.

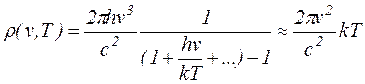Таким образом, в области малых частот закон Планка согласуется с классическими выражениями. Иначе обстоит дело в области больших частот. Если 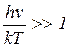, то экспонента в знаменателе гораздо больше 1. В этом случае единицей в знаменателе можно пренебречь и получим приближенный закон излучения для коротких волн (больших частот):

.

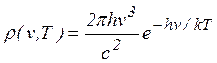Закон излучения в такой форме был предложен ранее Вином (1896 г.), который пытался феноменологически описать результаты своих измерений в этой части спектра. Между областями применимости этих двух предельных законов лежит обширная переходная область, где и находится максимум кривой распределения. При повышении температуры этот максимум в соответствии с законом Вина сдвигается в сторону более коротких длин волн.

Переходя к записи плотности излучения через длину волны 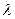, будем иметь

.

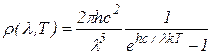Функция 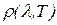имеет максимум при длине волны 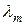, которую можно найти из условия

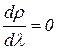
или

.

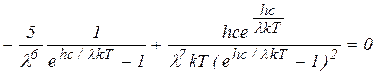Вводя 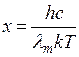, получим

, .

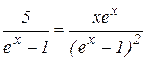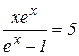Решение этого трансцендентного уравнения дает значение .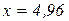

Таким образом,

.

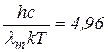Это и есть закон смещения Вина.

Постоянная Планка была впервые определена самим Планком с помощью закона Стефана и закона смещения Вина. Согласно первому закону, энергия, излучаемая за 1 с с квадратного метра нагретой до температуры 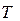поверхности, есть

,

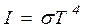где 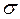– постоянная, называемая постоянной Стефана – Больцмана и равная

.

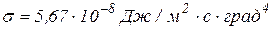Эту постоянную можно получить и теоретически, интегрируя по всему спектру функцию распределения Планка. В результате получим выражение для :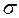

.

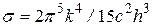С другой стороны, измерения показывают, что постоянная в законе Вина 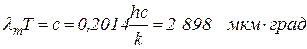. Чтобы найти порядок этой величины, достаточно заметить, что максимум интенсивности в излучении Солнца, которое излучает как черное тело, при температуре 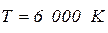лежит в зеленой части спектра, то есть приблизительно при 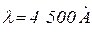. Зная эти две эмпирические постоянные, можно рассчитать 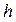и 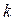. Найденные таким образом значения хорошо согласуются с оценками, полученными другими методами.

Из общего вида кривых распределения следует еще один вывод: – КПД, например, ламп накаливания и других осветительных приборов совершенно ничтожен. Действительно, область видимого света соответствует лишь узкой полосе в спектре теплового излучения, вся остальная энергия излучения пропадает даром для освещения.

Вернемся снова к истории открытия Планка. Его гипотеза встретила сначала яростное сопротивление физиков. Никто не хотел верить, что непременным условием вывода закона излучения является обращение к гипотезе квантов. Считалось, что новые идеи представляют собой просто математический прием и рано или поздно найдут классическую интерпретацию этого явления. Однако все попытки подобного рода потерпели провал.

Date: 2015-09-05; view: 283; Нарушение авторских прав