Волновая функция, ее физический смысл

Основная задача классической механики заключается в определении положения макрообъекта в любой момент времени. Для этого составляется система уравнений, решение которой позволяет выяснить зависимость радиуса-вектора 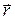от времени t. В классической механике состояние частицы при ее движении в каждый момент времени задается двумя величинами: радиус-вектором 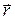и импульсом .

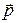Задать аналогичным образом состояние микрочастицы невозможно. Этому препятствует корпускулярно-волновой дуализм и соотношения неопределенностей Гейзенберга. С учетом наличия у микрочастицы волновых свойств ее состояние в квантовой механике задается с помощью некоторой функции координат и времени Y(x, y, z, t), называемой волновой или Y -функцией. Эта комплексная функция описывает состояние микрочастицы для любого момента времени. В случае одномерного движения частицы вдоль оси ОX волновая функция зависит лишь от координаты x и времени t, т.е. Y=Y(x, t). Для понимания физического смысла волновой функции обратимся к опытам по дифракции электронов. Оказывается, что четкие дифракционные картины обнаруживаются даже в том случае, если направлять на мишень одиночные электроны, т.е. когда каждый последующий электрон испускается после того, как предыдущий достигнет экрана. После достаточно продолжительной бомбардировки картина на экране будет в точности соответствовать той, которая получается при одновременном направлении на мишень большого числа электронов. Из этого можно сделать вывод, что движение любой микрочастицы по отдельности, в том числе и место ее обнаружения, подчиняются статистическим (вероятностным) закономерностям. При направлении на мишень одиночного электрона, точку экрана, в которой он будет зафиксирован, заранее со 100%-ной вероятностью предсказать невозможно.

В дифракционных опытах Томсона на фотопластинке образовывалась система темных концентрических колец. Можно с уверенностью сказать, что вероятность обнаружения (попадания) каждого испущенного электрона в различных местах фотопластинки неодинакова. В области темных концентрических колец эта вероятность больше, чем в остальных местах экрана. Распределение электронов по всему экрану оказывается таким же, каким является распределение интенсивности электромагнитной волны в аналогичном дифракционном опыте: там где интенсивность рентгеновской волны велика, частиц в опыте Томсона регистрируется много, а там, где интенсивность мала, – частицы почти не появляются. С волновой точки зрения наличие максимума числа электронов в некоторых направлениях означает, что эти направления соответствуют наибольшей интенсивности волны де Бройля. Это послужило основанием для статистического (вероятностного) истолкования волны де Бройля. Волновая функция как раз и является той величиной, которая позволяет отыскать все квантовые вероятности. Однако из всех этих вероятностей в дальнейшем рассмотрим лишь одну, описывающую вероятность распределения координаты частицы. Для одномерного движения вероятность dP обнаружения частицы в промежутке между точками x и x + dx в момент времени t равна

,

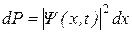где 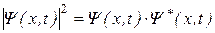– квадрат модуля волновой функции (значок *

обозначает комплексное сопряжение).

В общем случае движения частицы в трехмерном пространстве вероятность dP обнаружения частицы в точке с координатами (x, y, z) в пределах бесконечно малого объема dV задается аналогичным выражением: 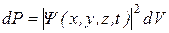. Впервые вероятностную интерпретацию волновой функции дал Борн (1926 г.)

Волновую, или Y -функцию, можно задавать с точностью до постоянного множителя. Если обозначить через A некоторую константу, то произведение А×Y определяет то же состояние частицы, что и Y.

Вероятность обнаружить частицу во всем бесконечном пространстве (если мы точно уверены, что частица существует) равна 1. Отсюда следует условие нормировки волновой функции:

.

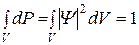Величина 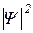является плотностью вероятности, или, что то же самое, плотностью распределения координат частиц. В простейшем случае одномерного движения вдоль оси OX среднее значение координаты вычисляется следующим образом:

.

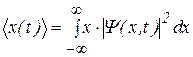Таким образом, точно предсказать в дифракционных опытах, в каком месте экрана будет зафиксирован тот или иной электрон, невозможно, даже заранее зная его волновую функцию. Можно лишь с определенной вероятностью предположить, что электрон будет зафиксирован в конкретном месте. В этом заключается отличие поведения квантовых объектов от классических. В классической механике при описании движения макротел мы со 100 % вероятностью заранее знали, в каком месте пространства будет находиться материальная точка (например космическая станция) в любой момент времени.

Date: 2015-09-05; view: 419; Нарушение авторских прав