Частица в потенциальной яме. Квантование энергии

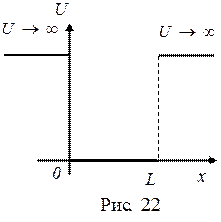Простейшим примером пространственно-ограниченного движения является одномерное движение квантовой частицы в силовом поле, имеющим вид очень глубокой потенциальной ямы с вертикальными стенками (рис. 22). В этом силовом поле график потенциальной энергии частицы U (x) имеет вид, показанный на том же рисунке. Непроницаемость стенок выражается в неограниченном возрастании U (x) в точках x = 0 и x = L.

Частица может находиться лишь на участке 0 < x < L. Значение потенциальной энергии частицы в пределах этого участка U (x) = 0. Так как частица не выходит из промежутка 0 < x < L, то вероятность ее обнаружения вне этого промежутка равна нулю, что возможно лишь в случае равенства нулю ее волновой функции вне этого участка. Следовательно, уравнение Шредингера должно быть дополнено граничными условиями: (0) = (L) = 0.

Решение уравнения Шредингера позволяет найти волновую функцию частицы в области 0 < x < L. Пусть силовое поле не меняется с течением времени, поэтому воспользуемся уравнением для стационарных состояний, которое в случае U = 0 принимает вид

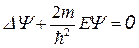. (9.2)

Для упрощения записи в дальнейшем введем в уравнение волновое число

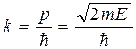, (9.3)

тогда уравнение (9.2) для одномерного случая приобретет вид

.

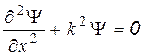Общим решением данного однородного дифференциального уравнения второго порядка является функция

,

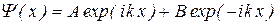где A и B – некоторые комплексные коэффициенты, не зависящие от x. Воспользуемся граничными условиями. Так как y (0) = 0, то A + B = 0 и, следовательно, B = - A и будем иметь

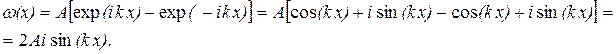
С учетом того, что y(L) = 0, получим 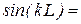0. Откуда 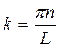, где n = 0, 1, 2, 3,… Случай n = 0 должен быть отброшен, так как при y(x) = 0, т.е. вероятность обнаружения частицы внутри ямы равна нулю. Однако с самого начала мы полагали, что частица локализована именно в области 0 < x < L. Чтобы показать, что волновое число k частицы принимает не непрерывный, а дискретный набор значений, волновому числу дописывают индекс n, т.е., записывают 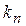. Так как волновая функция определяется волновым числом 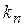, то и для нее используют тот же индекс n: y_n. Вместо A удобно ввести новую комплексную постоянную C = 2 iA, тогда

.

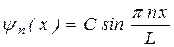Для нахождения амплитуды С волновой функции воспользуемся условием нормировки:

.

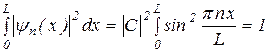Так как

,

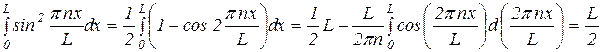то .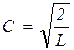

Таким образом, .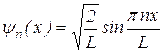

Из (9.3), выразив полную энергию частицы через волновое число 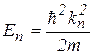, находим энергетический спектр частицы в бесконечно глубокой потенциальной яме: .

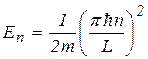Этот энергетический спектр дискретен. Во всем дискретном диапазоне значений энергии есть уровень, на котором энергия частицы минимальна. Этот уровень соответствует n = 1 и называется основным уровнем энергии. На этом уровне энергия частицы 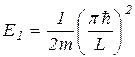> 0. Отсюда следует, что микрочастица не может обладать энергией, равной нулю, что означает невозможность остановки микрочастицы в классическом смысле.

10. РАДИОАКТИВНОСТЬ

Самопроизвольное (спонтанное) превращение нестабильных ядер в другие, сопровождающееся испусканием элементарных частиц и жесткого электромагнитного излучения, называется радиоактивностью.

К радиоактивным превращениям относятся альфа-распад ядер с массовым числом А в ядра с массовым числом А – 4 при одновременном испускании альфа-частиц, являющихся ядрами гелия (рис. 23).

Всe виды бета-распада ядер с порядковым номером Z в ядре Z + I (или Z – I) сопровождаются испусканием электрона, позитрона или захватом орбитального электрона (рис. 23, а).

При радиоактивном распаде существует вероятность образования ядра в возбужденном состоянии с последующим переходом в основное. При переходе ядра с верхнего энергетического уровня на нижний излучается гамма-квант с энергией, равной разности энергий уровней, между которыми происходит переход (рис.23, в). Радиоактивный распад атомных ядер как явление, происходящее в микромире, имеет случайную природу и может быть понят только на основе вероятностной интерпретации экспериментальных данных.

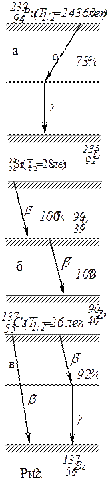Естественной статистической величиной, описывающей радиоактивный распад, является вероятность распада ядра в единицу времени 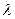. Эта величина называется также постоянной распада и является важнейшей характеристикой нестабильных (радиоактивных) ядер. Известно, что 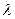в широких пределах не зависит от внешних факторов (температуры, давления и т.д.), в частности от начала отсчета времени.

Поэтому число распавшихся ядер 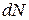в наблюдаемом временном интервале dt определяется только величиной этого интервала и числом ядер N в момент времени t. Экспериментальное соотношение, связывающее убыль радиоактивных ядер, имеет вид .

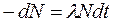Отсюда при условии, что 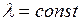в результате интегрирования и учета, что в момент времени t=0 число ядер было 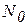, получим закон радиоактивного распада: .

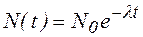Закон радиоактивного распада справедлив только для средних значений входящих в него величин. Интенсивность процесса радиоактивного распада характеризуют две величины: период полураспада 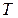и среднее время жизни 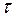радионуклида (нуклид – общее название атомных ядер, отличающихся числом протонов Z и нейтронов N).

Период полураспада 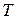– время, в течение которого распадается в среднем половина ядер. Эта величина определяется условием

,

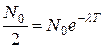откуда период полураспада ;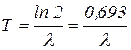

,

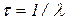которое совпадает со временем, в течение которого число радиоактивных ядер в системе убывает в 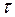раз. Это время не зависит ни от способа получения ядер, ни от внешних условий, в которых ядра находятся.

Интенсивность излучения бо-льшой совокупности радиоактивных ядер в целом характеризуется средним числом распадов в едини -

цу времени. Эта величина называется активностью.

В СИ единицей активности является беккерель: I Бк = I расп/с. Однако наиболее употребительной является внесистемная единица Кюри: I Ки = 3,7 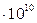расп./с.

Среднее число распадов в единицу времени, отнесенное к единице массы или объема вещества, называется удельной активностью.

Удельная активность может быть выражена различными единицами измерений: Бк/мл, Бк/г, Бк/см³, Бк/л, Ки/кг и т.д. Именно активность образца является той величиной, которая непосредственно может быть измерена экспериментально. Очевидно, что активность А убывает со временем также по экспоненциальному закону:

.

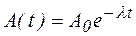Date: 2015-09-05; view: 577; Нарушение авторских прав