Теоретические сведения. Установлено, что при медленном течении газа по трубке небольшого сечения под действием постоянной внешней разности давлений он движется слоями

Установлено, что при медленном течении газа по трубке небольшого сечения под действием постоянной внешней разности давлений он движется слоями. Скорость слоя прилегающего к стенкам капилляра в результате прилипания молекул близка к нулю. На оси капилляра скорость газа максимальна. Вследствие хаотического (теплового) движения молекул между движущимися друг относительно друга слоями газа происходит постоянный обмен молекулами. Это приводит к переносу от слоя к слою определенного количества движения от центрального слоя газа, где скорость наибольшая, к слоям, движущимся с меньшей скоростью. В результате чего медленные слои ускоряются, а более быстрые замедляются. Такое взаимодействие слоев газа (жидкости) препятствующее перемещению одного слоя относительно другого называется вязкостью (внутренним трением). Количественно вязкость определяется величиной касательной силы, которая должна быть приложена к площади сдвигаемого слоя, Чтобы поддерживать в этом слое ламинарное течение.

Ламинарным течением называется движение газа (жидкости) движущегося параллельными слоями с градиентом скорости, перпендикулярным направлению движения молекул. Вязкость газа не зависит от его плотности (давления), т.к. при сжатии газа общее количество молекул, переходящих из слоя в слой, увеличивается, но зато каждая молекула менее глубоко проникает в соседний слой и переносит меньшее количество движения. Для очень разряженных газов понятие вязкости теряет смысл.

Французским ученым Ж.Л.М. Пуазейлем был установлен закон течения жидкости в тонкой цилиндрической трубке, названный законом Пуазейля: объем V жидкости, протекающий через поперечное сечение трубки, прямо пропорционален разности давлений p и p₀ на концах капилляра, четвертой степени диаметра d трубки, времени протекания t и обратно пропорционален длине трубки и коэффициенту вязкости:

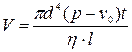(8.1)

Закон Пуазейля применим только при ламинарном течении (практически для очень тонких трубок или капилляров) и при постоянной разности давлений на концах трубки.

Закон Пуазейля используют для определения вязкости жидкостей и газов. Пропуская жидкость или газ через трубку известного радиуса измеряют перепад давления и поток. Затем, используя полученные данные, вычисляют коэффициент вязкости .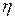

Закон Пуазейля применим к жидкостям и газам при условии, что плотность среды в процессе движения не испытывает сколь-нибудь заметного изменения, так что ее можно считать постоянной. В таких случаях движущуюся среду называют несжимаемой. Хотя с обычной точки зрения газ является легко сжимаемой средой, но те изменения давления, которые возникают в газе при его движении, обычно недостаточны для сколько-нибудь существенного изменения его плотности. Газ перестает вести себя как несжимаемая среда лишь при скоростях сравнимых со скоростью звука.

Описание установки

Рисунок 8.1 – Установка для определения коэффициента вязкости воздуха

Б – стеклянный баллон с водой

М – манометр

К – капилляр

1,2 – тройники

3,4 – соединительные трубки.

Установка для определения коэффициента динамической изображена на рис.8.1. При открытом кране баллона из него вытекает вода. При этом давление в баллоне уменьшается и в него будет засасываться воздух, который будет проходить через капилляр. Один конец капилляра, через который протекает воздух, с помощью тройника 1 соединяется с атмосферой и правым коленом манометра. Другой конец капилляра с помощью тройника 2 соединяется со стеклянным баллоном и левым коленом манометра. Т.о. разность давлений на концах капилляра равна разности давлений в баллоне и атмосферным. Эту разность можно измерить с помощью манометра .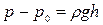

Течение воздуха при небольших скоростях будет ламинарным. Для случая установившегося ламинарного течения воздуха параметры, характеризующие течение (скорость и давление в различных точках потока)
не меняются с течением времени. В данной работе измерения проводятся при небольших разностях давлений на концах капилляра и, следовательно для определения коэффициента вязкости можно применить закон Пуазейля (8.1).Выразим из (8.1) коэффициент вязкости :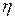

(8.2)

Выполнение измерений

1. Наполните баллон на ¾ объема и плотно закройте пробкой.

2. Подставьте сосуд для выливающейся воды. Откройте кран (вода не должна капать). Подождите, пока разность уровней жидкости в коленах манометра перестанет изменяться.

3. При установившемся течении воздуха через капилляр (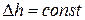) запишите разность 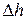. Подставьте под вытекающую струю воды мерный стакан и одновременно включите секундомер. Измерьте время, за которое из баллона вытекает заданный преподавателем объем воды.

4. Результаты измерений занесите в таблицу. Повторите измерения три раза.

5. Проведите измерения для других значений объема.

6. По формуле рассчитайте разность давлений 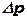.Результаты измерений и вычислений занесите в таблицу.

7. По формуле (8.2) вычислите коэффициент динамической вязкости воздуха.

8. Повторите опыт п.п.2-6 для других заданных преподавателем объемов.

Таблица 8.1

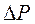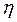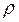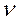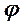№ п/п	h, см	t, с	, Па	, Н.с/м2	T, К	P, Па	, кг/м3	, м2/с	, м2/ Н.с

Дополнительные данные:

r = 0,585 мм; l = 116,5 мм; 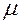= 29 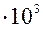кг моль^-1

Вопросы для самоконтроля:

1. Что такое вязкость?

2. Какое течение газа (жидкости) называется ламинарным?

3. Запишите и сформулируйте закон Пуазейля.

4. От чего зависит коэффициент вязкости газов?

5. Чем объяснить, что вязкость жидкостей и газов зависит от температуры неодинаково?