
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Очевидно, что курс уменьшается вместе с ростом рыночной ставки и срока облигации
|
|
Облигации с выплатой процентов и номинала в конце срока. Общая сумма, которую получает владелец облигации при ее погашении, равна N(\ + g)n. Соответственно расчетная цена и курс при ставке помещения / составят
(I + g\n (I + g\n
Из последней формулы следует, что курс определяется тремя параметрами, причем влияние срока зависит от соотношения ставок g и /. Если g > /, то, как видим, с увеличением срока курс экспоненциально растет.
ПРИМЕР 11.11. Пусть текущий доход от облигации выплачивается вместе с номиналом в конце срока; п = 5, д = 8% (начисление процентов поквартальное), / = 12%. В этом случае
/(1 +0,08/4)4\5 «-(1+0,12) 100 = 84'32-
Облигации с периодической выплатой процентов и погашением номинала в конце срока. Напомним, что доход от таких облига-
ций имеет два источника — периодически получаемые проценты и разность между ценой приобретения и выкупной ценой. Необходимые равенства для определения цены и курса таких облигаций были найдены выше (см. (11.6)—(11.10)).
| ПРИМЕР 11.12.Для облигации примера 11.11 при условии, что проценты выплачиваются поквартально, находим согласно (11.8) | ||||
| К = | [(1 +0.12)"5 | + 0,08а(5^12]100. | ||
| Поскольку | а(4) = 35;12 | 1 - 1,12" | по- | |
| ' 4(1,121/4- | - 3,76316, окончательно | |||
| лучим К = | 86,85. |
Для определения расчетного курса по формулам (11.7) и (11.9) можно применить программу ПЗ пакета Excel (см. с. 110—111).
Влияние факторов. Посмотрим, как влияют различные факторы на курс облигации. Для этого вернемся к равенству (11.7):
Очевидно, что изменение купонной процентной ставки влияет только на второе слагаемое. Так, рост этой ставки увеличивает данное слагаемое и курс в целом, причем это увеличение линейно: чем больше рыночная ставка, тем это влияние меньше при всех прочих равных условиях.
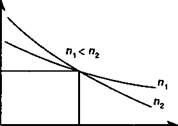
Что касается влияния рыночной ставки процента или ставки помещения, учитываемой в расчете, то повышение этой ставки приводит к сокращению обоих слагаемых курса облигации. Зависимость курса от размера рыночной ставки показана на рис. 11.3, на основе которого можно сделать один важный в практическом отношении вывод: чем больше срок облигации, тем чувствительней курс к изменению рыночной ставки (круче кривая).
Сказанное объясняет тактику поведения инвесторов на рынке облигаций. Так, если ожидается повышение рыночной ставки, то инвесторы стремятся заменить долгосрочные облигации на облигации с меньшим сроком. При ожидании снижения ставки происходит обратное.
Степень влияния уровня рыночной ставки на курс облигации зависит и от размера купонной нормы дохода — чем она выше, тем меньше влияет изменение ставки. Указанная зависимость лежит в основе следующего правила поведения инвесторов: при ожидании повышения рыночной ставки для инвестора предпочтительней покупать облигации с высокой купонной доходностью и, наоборот, при понижении ставки для инвестора целесообразно вкладывать деньги в облигации с низкой купонной доходностью.
|
к
Рис. 11.3
Перейдем к влиянию срока облигации. С увеличением срока величина первого слагаемого курса падает, второго растет при всех прочих равных условиях. Суммарный результат зависит от того, в каком соотношении находятся норма купонного дохода и рыночная ставка процента (см. рис. 11.4). На этом рисунке показано, что при g > i сокращение первого слагаемого перекрывается ростом второго. При равенстве нормы купонного дохода рыночной ставке изменения слагаемых курса полностью компенсируют друг друга.
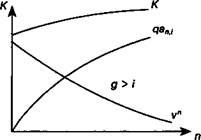
Рис. 11.4
Проблема оценивания облигаций существует не только тогда, когда облигация покупается или продается на рынке, но и когда она находится у владельца. В общем случае ее цена изменяется во времени даже в такой крайне редкой ситуации, когда рыночная процентная ставка остается постоянной и уж тем более, если эта ставка изменяется. С приближением даты погашения увеличивается современная стоимость суммы, получаемой при погашении облигации, одновременно уменьшается современная стоимость будущих поступлений по купонам. Какой бы ни была цена до погашения, в конце срока цена облигации равна номиналу или некоторой заранее фиксированной выкупной цене.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Четыркин КМ. Методы финансовых и коммерческих расчетов. М.: Дело, 1995. Гл. П.
2. Кристина И. Рынок облигаций. М.: Дело, 1999. Гл. 5.
3. Cartledge P. Financial arithmetic. A practitioners guide. Euromoney Books, 1993. Ch 5, 6.
Date: 2015-09-19; view: 507; Нарушение авторских прав