Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Из последней формулы следует
|
|
| /-ilL-i. (11.5) |
| "'100 |
10(Если курс облигации меньше 100, то / > g.
ПРИМЕР 11.3. Облигация, приносящая 10% годовых относительно номинала, куплена по курсу 65, срок до погашения 3 года. Если номинал и проценты выплачиваются в конце срока, то полная доходность для инвестора составит
«0,26956, или 26,956%.
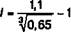
Облигации с периодической выплатой процентов и погашением номинала в конце срока. Этот вид облигаций получил наибольшее распространение в современной практике. Для такой облигации можно получить все три показателя доходности — купонную, текущую и полную. Текущая доходность рассчитывается по полученной выше формуле (11.2). Что касается полной доходности, то для ее определения необходимо современную стоимость всех поступлений приравнять цене облигации. Поскольку поступления по купонам представляют собой постоянную ренту постну-мерандо, то член такой ренты равен gN9 а современная ее стоимость составит gNan.n если купоны оплачиваются ежегодно, и gN(№.r если эти выплаты поизводятся р раз в году, каждый раз по ставке g/p. Дисконтированная величина номинала равна Nvn. В итогб получим следующие равенства. Для облигации с годовыми купонами
Р «Nvn +gN^v* «Nvn + gNan.h (11.6)
l
Откуда
Для облигации с погашением купонов по полугодиям и поквартально часто применяют
где a(pJ.. — коэффициент приведения /ьсрочной ренты (р = 2, Р = 4)Я,/.
Во всех приведенных формулах Vя означает дисконтный множитель по неизвестной годовой ставке помещения /.
Б зарубежной практике, однако, для облигаций с полугодовыми и квартальными выплатами текущего дохода для дисконтирования применяется годовая номинальная ставка, причем число раз дисконтирования в году обычно принимается равным числу раз выплат купонного дохода (р = /и). Таким образом, исходное для расчета ставки помещения равенство имеет вид
где у — номинальная годовая ставка, рп — общее количество купонных выплат, g — годовой процент выплат по купонам.
Искомые размеры ставок (/ nj) в формулах (11.8) и (11.9) несопоставимы, так как получены для разных условий: т = 1 и т = р.
При решении приведенных выше равенств относительно неизвестной величины / или J сталкиваются с такими же проблемами, что и при расчете / по заданной величине коэффициента приведения ренты (см. § 5.3). Искомые значения ставки помещения рассчитываются или с помощью интерполяции, или каким-либо итерационным методом. В одной из версий пакета Excel содержится программа ДОХОД (Yield) для расчета /.
Оценим / с помощью линейной интерполяции:
/=/'+ к,1K„(i"-i% (НЮ)
где Г и /" — нижнее и верхнее значения ставки помещения, ограничивающие интервал, в пределах которого как ожидается находится неизвестное значение ставки, К\ К'1 — расчетные значения курса соответственно для ставок /', /". Интервал ставок для интерполяции определяется с учетом того, что / >g при К < 100.
В финансовой литературе иногда рекомендуют метод приближенной оценки, согласно которому
£+(l------- —)/п
{ 100J'
В этой формуле средний годовой доход от облигации соотносится со средней ее ценой. За простоту расчета, впрочем, приходится платить потерей точности оценки. Чем больше курс отличается от 100, тем больше погрешность.
ПРИМЕР 11.4. Облигация со сроком 5 лет, проценты по которой выплачиваются раз в году по норме 8%, куплена по курсу 65.
Текущая доходность по облигации: 8/65 = 0,12308.
Для расчета полной доходности запишем исходное равенство (см. (11.7)):
0,65 = (1 +/Г5 + 0,08а5;/. Приближенное решение по (11.11) дает
/= В+ (100-65)/5
(100+ 65)/2 u»,ol°*-
Проверка: при данной величине доходности рыночный курс составит
-^ = 1,18182-5 + 0,08а5.18182 = 0,6829.
Курс заметно выше 65 — как видим, доходность занижена. Положим, что искомая ставка находится в интервале 12,5 + 20%. Соответственно получим К' = 0,83977 и К" = 0,64113. По интерполяционным формулам находим:
83,977 - 65 /=12'5+ 83,977 - 64,113 (И» - 12,5) = 19,66%.
Курс при такой ставке составит 64,87. Расчетный курс весьма близок к рыночному, и, следовательно, данная оценка ставки точнее, чем оценка 18,18%. Точная величина / = 19,62%.
Все рассмотренные выше формулы для расчета полной доходности предполагают, что оценка производится на начало срока облигации или на дату выплаты процентов при условии, что проценты на эту дату уже выплачены. Для случая, когда оценка производится на момент между двумя датами выплат процентов, приведенные формулы дадут смещенные оценки, так как не учитывают накопленные проценты. Необходимо принять во внимание, что срок погашения и выплат процентов до момента оценки сокращается. Доходность в этом случае можно определить на основе следующего равенства:
где к — доля купонного периода, d — количество оставшихся купонов.
Date: 2015-09-19; view: 529; Нарушение авторских прав