
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение, как видим, сводится к нахождению корня этого уравнения
|
|
| ПРИМЕР 7.2. Исходные данные: F Соответственно имеем | = 100, p = | 50, с = 40, h | = 0,5. | ||
| 50Qk - 40Q°'5 - | - 100 | = 0. | |||
| Найдем корни этого уравнения. квадратное, положив О = z2. После | Для чего | этого преобразуем получим | его в | ||
| *«-■ | 50z2 - 40z - | 100 = | = 0, | ||
| -(-40)±^40)2 27 | -4х! 50 | 50 х(- | -юо) | ||
| Положительный = 1,862 = 3,46. | корень равен | 1,86. | Таким образом, | °*= |
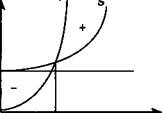
Перейдем к сочетанию двух нелинейных зависимостей. Например, пусть обе функции являются параболами второй степени (см. рис. 7.4). Тогда
V= aQ2 + bQ, S=cQ2 + dQ +F,
где a, b, c, d — параметры парабол.
Прибыль в зависимости от уровня выпуска составит
Р = {а - c)Q2 + {b-d)Q- F (7.5)
Барьерный объем выпуска находится как корень квадратного уравнения
(a-c)Q2k + (b-d)Qk-F=0. 154
|
V, s
F
 Ok 0
Ok 0
Рис. 7.4
Добавим, что при некоторых условиях можно рассчитать объем выпуска, максимизирующего размер прибыли (обозначим его как Qm). Для этого, как известно, достаточно найти производную функции прибыли и приравнять ее нулю. В случае, когда прибыль описывается выражением (7.S), находим
g»-t^t- <7-6>
Как видим, положение точки максимума полностью определяется параметрами соответствующих парабол. Причем необходимым условием существования максимума являются следующие соотношения: d>b, a>c. Если же b>d и а>с, то прибыль монотонно растет вместе с увеличением выпуска.
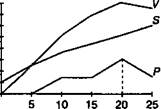
Нелинейную модель можно представить и в неформализованном виде — как таблицу данных, характеризующих затраты и стоимость продукции в зависимости от размера выпуска (см. пример 7.3).
ПРИМЕР 7.3. В приведенной ниже таблице и на диаграмме содержатся данные о затратах, стоимости продукции и ожидаемой прибыли.
| о | F | с | Р | S | V | Р |
| — | — | — | — | |||
 V, S, P
V, S, P
|
700-
600-
500-
300-
100-
Date: 2015-09-19; view: 405; Нарушение авторских прав