Изменение параметров рент

Изменение хотя бы одного условия ренты по существу озна­чает замену одной ренты другой. Как уже отмечалось выше, та­кая замена должна базироваться на принципе финансовой эк­вивалентности. Из этого следует равенство современных стои­мостей обеих рент. Что касается процентной ставки, то она мо­жет быть сохранена или изменена. Например, кредитор в обмен на увеличение срока может потребовать некоторого ее увеличе­ния. Отправляясь от указанного равенства, нетрудно опреде­лить параметры заменяющей ренты. Рассмотрим несколько случаев такой замены.

Замена немедленной ренты на отсроченную. Пусть имеется не­медленная рента постнумерандо с параметрами Л,, п_{9 процент­ная ставка равна /. Необходимо отсрочить выплаты на t лет. Иначе говоря, немедленная рента заменяется на отсроченную с

параметрами R_v я₂, t (t не входит в срок ренты). Здесь возмож­ны разные постановки задачи в зависимости от того, что задано для новой ренты. Если задан срок, то определяется Л₂, и наобо­рот. Рассмотрим первую задачу при условии, что п₂ = л, = я. Для этого случая справедливо следующее равенство:

Откуда

Л₂=Л_|(1+/У. (6.37)

Иначе говоря, член новой ренты равен наращенному за вре­мя t члену заменяемой ренты.

В общем случае, когда п₂* я,, из равенства А_х = А₂ следует

R₂. ^^-(l+i)', (6.38)

^an₂\i

где / — продолжительность отсрочки.

ПРИМЕР 6.13. Пусть немедленная рента постнумерандо с усло­виями Я₁ = 2 млн руб. и сроком 8 лет откладывается на 2 года без изменения срока самой ренты. Процентная ставка, принятая для пролонгирования, — 20% годовых. Согласно (6.37) получим

Я₂ = 2 х 1,2² = 2,88 млн руб.

Таким образом, отказ от выплаты немедленной ренты увели­чивает ежегодные выплаты на 0,88 млн руб. Если же одновремен­но со сдвигом начала выплат срок ренты увеличивается, скажем, до 11 лет вместо 8 (л = 11), то по формуле (6.38) находим

*2 = ^Т^ ^{х 1}'^{22 = 2 х} !'!от^ ^{х 1}'^{22 = 2}'^{55393 млн} РУ⁶'

^а11;20 4,32706

Определим теперь срок новой ренты при условии, что раз­мер члена ренты остается без изменений. Пусть выплата ренты откладывается на / лет. Тогда из равенства

Я**,;/ - ^Кап₂-У находим 144

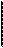
-In{l -[!-(!+ /Г1(1 + т ₍,,_оч

"2 ⁼-------------- щПЦ -------------- ■ ⁽⁶³⁹⁾

ПРИМЕР 6.14. Рента с условиями Я = 2 млн руб., п = 5 лет, / = 8% откладывается на три года без изменения сумм выплат. Необходимо найти новый срок и сбалансировать результат. По формуле (6.39) получим

-1п[1 -(1 - 1,08-⁵)1,08³]

п₀ =------------- ■------ ■ ---- ——- = 6,689 года.

² In 1,08 ' ^д

Таким образом, отказ от немедленной выплаты ренты обой­дется в 1,7 года увеличения срока ренты. Пусть продолжитель­ность новой ренты (без учета отсрочки) равна 6 годам. Современ­ная стоимость такой ренты с учетом отсрочки равна

А₂ = Ra_ssv3 = 2000 х 4,6288 х 1.08"³ = 7339,58 тыс. руб.

Однако у заменяемой ренты современная стоимость равна 7985,42 тыс. руб. Разность в сумме 645,84 тыс. руб. следует уп­латить в начале действия контракта или с соответствующим нара­щением в любой иной момент.

Замена годовой ренты на /^-срочную. Пусть годовая немедлен­ная рента с параметрами Л,, п_{ заменяется на р-срочную с па­раметрами R₂, n₂, р. Если заданы срок заменяющей ренты, ее периодичность и ставка, то

*2-*i%. (6.40)

_а(Р)

Причем, если п₂ = п_{ = я, то

«*/ />[(!+О'/'-1]

*«

Откуда

R₂ - Л,—------ J------ Ц (6.41)

ПРИМЕР 6.15. Пусть Я₁ = 2, п₁ = п₂ = п. Если годовая рента по-стнумерандо заменяется, скажем, на квартальную, то при неиз-

менности срока ренты эквивалентность замены достигается толь­ко за счет корректировки размера выплат. При условии, что / = = 20%, находим

4(1 2^1/4 - 1)
Я₂ = 2 х '₀₂--------- ^L = 1,86541.

Продолжим пример. Пусть теперь п₁ = 3, а п₂ = 4 года. Соглас­но (6.40) получим

^аз;20 2,10648

^{Я2 = 2}^^=2Х^^^=1,51791'

Замена годовой ренты на р-срочную может быть осуществле­на и при условии, что заданным является размер члена ренты. Определяется ее срок. В общем случае для этого сначала нахо­дим

>),. Л -£*,:, (6-42)

2 ^К2