Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
С постоянным относительным
|
|
Приростом платежей
Рассмотрим ситуацию, когда платежи изменяют свои размеры во времени с постоянным относительным ростом, т.е. следуют геометрической прогрессии. Поток таких платежей состоит из членов Л, Rq, /?^2,..., Rqn~x (q — знаменатель прогрессии или темп роста). Пусть этот ряд представляет собой ренту постнумерандо. Тогда ряд дисконтированных платежей состоит из величин Rv, Rqv1,..., Rqn~xvn. Получена геометрическая прогрессия с первым членом Rv и знаменателем qv. Сумма членов этой прогрессии равна
q"v" — 1 (qv)" — 1
А = Rv* --------- - = R w > (6л3)
qv 1 q- (1 + i)
Пусть теперь q = 1 + к, где к — темп прироста платежей. После простых преобразований получим
_,1 + к)"
A = R ----- :_ к . (6.14)
Заметим, что прирост может быть как положительным (к > 0), так и отрицательным (к < 0).
Наращенная сумма ренты находится как
а" - (1 + i)"
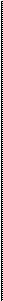_ „о+*>-_<■+.г (615)
Gt; I
ПРИМЕР 6.3. Несколько изменим условия примера 6.1. Пусть теперь члены ренты увеличиваются каждый год на 12% (/с = 0,12). В этом случае
(0,9У°
'-■Л2 А = 15 х Q2_012 = 93,448 млн руб.,
1,1210- 1,210
S = 15 х — = 578,604 млн руб.
I, it ■" I,^
Допустим теперь, что платежи уменьшаются во времени с темпом прироста минус 10% в год (к = -0,1), тогда
<-(С
А = 15 х Q2-/-Q ц = 47,184 млн руб., S = 47,184 х 1,210 - 292,151 млн руб.
Для годовых рент пренумерандо получим
/1 + к)"
(qv)" - 1 U + '>
А = *W; . (1 + 0 = R --------- 1 --- Н-(1 + 0. (6-16)
qv — 1 л — /
(ov)" ~ 1 V1 + ',
5 = R— —— (1 + 0я = R --------- т--- =-Hl + 0я+|. (6.17)
qv — 1 Ас — /
Рента р-срочная с постоянными опюопельными изменениями членов. Пусть платежи производятся не один, а р раз в году пост-нумерандо, проценты начисляются раз в году по ставке /. В этом случае последовательность платежей представляет собой геометрическую прогрессию Я, Rq,..., Rq"?"1, где q — темп роста за период. Начислим проценты и суммируем результат, получим
qnp - Л + /)я
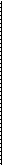Для современной величины такой ренты находим
Qnpvn _ J
ПРИМЕР 6.4. Пусть Я = 15 млн руб., п = 10, / = 20%. Положим, что платежи увеличиваются с каждым полугодием на 6%. Тогда наращенная сумма и современная стоимость ренты постнумеран-до составят:
1.0620- 1,210 S = 15 х 1 QQ , 1 2о,5 = 1263,052 млн руб.,
^Об^х 1,2"10- 1
А = 15 х------- 1 QQ . 1 20,5---------- = 203,990 млн руб.
Date: 2015-09-19; view: 401; Нарушение авторских прав