Задача 1.1 (3)

Найти уравнения движения точки М обода колеса радиуса R вагона, который движется по прямолинейному участку пути со скоростью V. Колесо катится без скольжения. Точка М в начальный момент движения соприкасалась с рельсом, т.е. занимала положение М₀ (рис. 1.1).

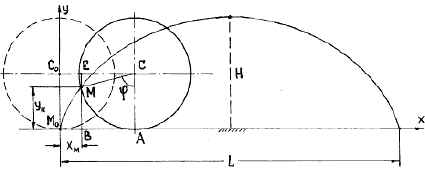
Рис. 1.1

Решение

Изобразим на расчетной схеме (рис. 1.1) оси координат х и у, начало координат поместим в начальное положение точки М₀.

Рассмотрим два положения колеса: в начальный момент t = 0 и в текущий момент времени t.

Отметим положение точки М на ободе колеса и положение центра С колеса в момент t, координаты точки: x_м = М₀В, у_м = МВ.

Расстояние от центра колеса до рельса остается постоянным и равным R; это значит, что центр C колеса движется по прямой, параллельной оси х. За время t центр колеса переместится на расстояние C₀C = Vt (закон равномерного движения точки C), одновременно колесо повернется на угол j.

Чтобы получить уравнения движения точки М, надо координаты этой точки представить как функции времени.

Из расчетной схемы (рис. 1.1) видно, что

х_м = C₀C – ЕС, у_м = ВЕ – МЕ;

или

х_м = Vt – ЕС, у_м = R – МЕ.

Из треугольника МЕС имеем;

МЕ = Rsin (90° – j) = Rcosj,

ЕC = Rcos (90° – j) = Rsinj,

Тогда х_м = Vt – Rsinj, (a)

у_м = R – Rcosj.

Найдем зависимость угла j от времени t: так как колесо катится без скольжения, то длина дуги АМ окружности обода колеса (рис.1.1) равна длине отрезка М₀А.

При этом

М₀А = С₀С = Vt,

но длина дуги АМ равна также произведению радиуса R на центральный угол j; поэтому Vt = Rj, отсюда .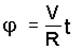

Теперь уравнения (а) будут иметь вид

; .

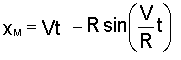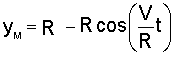Полученные уравнения представляют собой уравнения движения точки М. В аналитической геометрии показано, что это параметрические уравнения циклоиды (параметром в данном случае является время t). Таким образом, траектория точки обода колеса, движущегося по прямолинейному участку пути без проскальзывания, является циклоидой. Длина одной ветви циклоиды L (рис. 1.1) равна 2p R, высота – H = 2R.

Date: 2015-09-18; view: 627; Нарушение авторских прав