Кинематика точки

В задачах данного раздела определяются координаты, скорость, ускорение точки в любой назначенный момент времени при различных способах задания движения. Из всех способов задания движения точки наибольшее распространение получили координатный и естественный способы.

Рассмотрим вначале координатный способ задания движения точки. Положение в пространстве движущейся точки определяется тремя координатами в декартовой системе координат. Эти координаты задаются как функции времени:

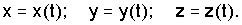(1.1)

Зависимости (1.1) называются уравнениями движения точки в декартовых координатах.

Если движение точки происходит в плоскости ху, то задаются только два уравнения движения:

x = x(t); y = y (t).

При прямолинейном движении точки достаточно задать одно уравнение движения:

x = x(t),

если принять, что ось х совпадает с прямой, по которой движется точка.

Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени.

При задании движения точки уравнениями (1.1) проекции скорости на оси декартовых координат равны:

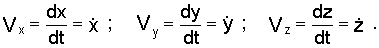
Модуль скорости

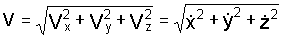. (1.2)

Направление скорости определяется направляющими косинусами:

.

Если движение точки задается в плоскости ху, то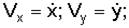

.

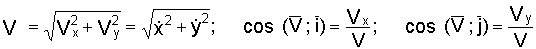При прямолинейном движении по оси х:

.

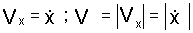Характеристикой быстроты изменения скорости является ускорение` а. Ускорение точки равно производной от вектора скорости по времени:

.

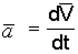При задании движения точки уравнениями (1.1) проекции ускорения на координатные оси равны:

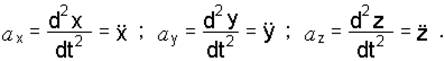
Модуль ускорения:

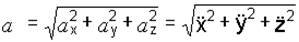. (1.3)

Направление ускорения определяется направляющими косинусами

; ; .

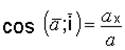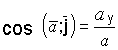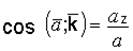Если движение точки задается в плоскости ху, то ;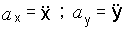

; ; .

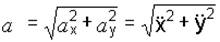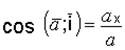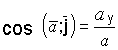При прямолинейном движении по оси х

; .

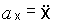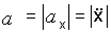Далее рассмотрим естественный способ задания движения точки.

Считается, что движение точки задано естественным способом, если указаны ее траектория и закон изменения криволинейной координаты s = s(t). Уравнение s = s(t) называется законом движения точки по траектории. При этом на траектории указывается начало отсчета, а также положительное направление отсчета координаты s в виде стрелки .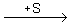

Модуль скорости точки определяется по формуле

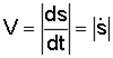. (1.4)

Вектор скорости` V направлен по касательной к траектории в сторону стрелки 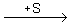, если 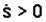, и в противоположную сторону, если .

Ускорение точки определяется как векторная сумма касательного и нормального ускорений точки:

` а =` аt +` а _n.

Модуль касательного ускорения определяется по формуле

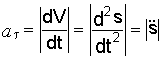. (1.5)

Вектор касательного ускорения` аt направлен по касательной к траектории в сторону стрелки 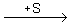, если 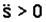, и в противоположную, если .

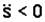Модуль нормального ускорения определяется по формуле

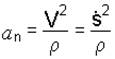, (1.6)

где r – радиус кривизны траектории в данной точке.

Вектор нормального ускорения` а _n всегда направлен по главной нормали в сторону центра кривизны траектории.

Модуль полного ускорения

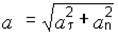. (1.7)

Если движение точки задано координатным способом, то можно определить параметры движения, характерные для естественного способа задания движения.

Так можно, например, по уравнениям движения точки (1.1) найти уравнение ее траектории в форме зависимости между координатами. Для этого надо из уравнений движения исключить время t. Затем можно найти закон движения точки по траектории s = s(t), используя формулу (1.4). Из этой формулы следует, что ds = V dt; с учетом формулы (1.2) имеем 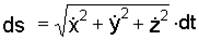и

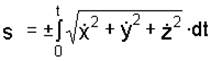. (1.8)

В законе движения (1.8) за начало отсчета координаты s принимается начальное положение точки, когда t = 0. Знак “плюс” или “минус” перед интегралом ставится в зависимости от выбора положительного направления отсчета координаты s: если движение точки начинается в сторону стрелки 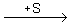, то следует брать знак “плюс”, в противном случае – знак “минус”.

Рассмотрим вначале методику решения задач, в которых движение точки задано координатным способом. Уравнения (1.1) определяются либо из геометрических условий, либо в результате интегрирования дифференциальных уравнений движения точки. Интегрирование дифференциальных уравнений движения точки рассматривается в разделе “Динамика точки”, который не входит в данное пособие. Получение уравнений (1.1) с использованием геометрии движения рассмотрим на примере исследования движения точки обода колеса.

Задача 1.1 (3)

Задача 1.2 (1)

Задача 1.3 (2)

Задача 1.4 (4)

Задача 1.5 (4)

Задача 1.6 (5)

Задача 1.7 (6)

Задача 1.8 (7)

Date: 2015-09-18; view: 439; Нарушение авторских прав