Завдання №5

Задача 26.2. Вантажі А і В приводяться в рух за допомогою двох блоків: рухомого К і нерухомого L (див. рис. 26.2). В результаті поштовху, наданого вантажу А, він почав опускатися зі швидкістю v₀.

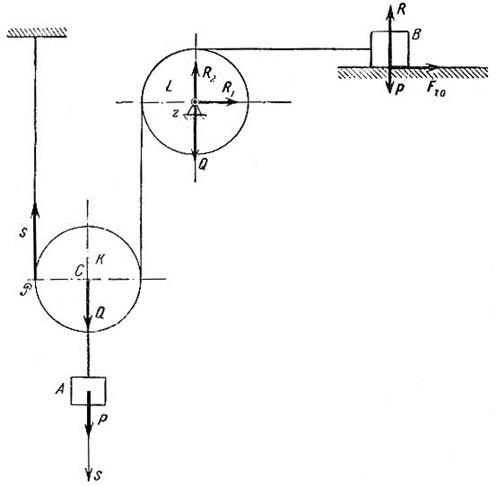На яку відстань повинен опуститися вантаж А для того, щоб його швидкість збільшилась у два рази? Вантажі А і В однакової ваги. Блоки К і L вважати однорідними круглими дисками однакової ваги Q. Коефіцієнт тертя ковзання вантажу В об горизонтальну площину дорівнює f. Масою нитки знехтувати.

Розв'язання:

Запишемо теорему про зміну кінетичної енергії системи матеріальних точок :

Так як мотузка охоплює блоки K і L і приводить в рух вантаж В, не деформується і при русі системи знаходиться в натягнутому стані, то розглядувана матеріальна система є незмінною. Отже, сума робіт внутрішніх сил сиситеми дорівнює нулю. Тому (1) набуває вигляду:

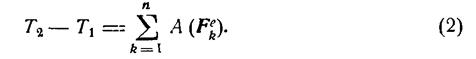
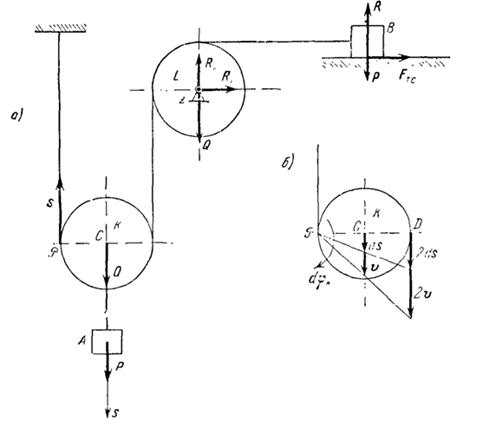Зобразимо зовнішні сили системи: сили тяжіння вантажів А і В і блоків K і L, R - нормальну силу реакції в горизонтальній площині, 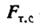- силу тертя ковзання вантажу В об горизонтальну площину 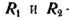- складові сили реакції осі блоку L, S - силу реакції мотузки.

Дамо елементарне переміщення ds центру інерції З блоку К по вертикалі вниз. При цьому блок К отримає кутове переміщення за годинниковою стрілкою. Враховуючи, що блок К, що здійснює плоский рух, має миттєвий центр швидкостей 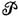в точці дотику блоку з лівою гілкою мотузки, знаходимо переміщення точки обода D, рівне 2ds. Отже, елементраное переміщення вантажу В направлено по горизонталі наліво і одно 2ds, а кутове переміщення блоку L спрямоване проти годинникової стрілки.

Обчислимо елементарну роботу всіх зовнішніх сил системи:

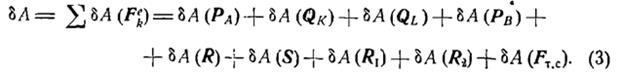
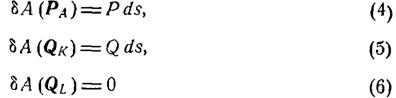Знаходимо:

(Точка прикладання ваги 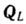, неподвижна),

(Груз В переміщається по горизонталі),

(Сила реакції мотузки S завжди прикладена в миттєвому центрі швидкостей ),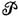

(Нормальна сила реакції R перпендикулярна до елементарного переміщенню вантажу В),

(Точка прикладання сил 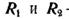неподвижна),

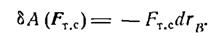
Так як переміщення вантажу спрямоване наліво 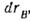, так само 2ds, а 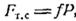, то

Після підстановки виразів (4),(5),(6),(7),(8),(9),(10) і (11) у формулу (3) знаходимо:

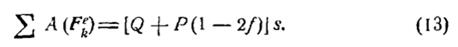Для обчислення роботи на шуканому переміщенні вантажу А, рівному s, випливає, скориставшись формулою (12), взяти визначений інтеграл в межах від 0 до s.Тоді будемо мати:

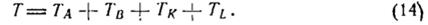Перезходимо до обчислення кінетичної енергії системи, до складу якої входять маси двох вантажів і двох блоків. запишемо:

Обозначим через скорость груза А. Тоді 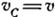. Враховуючи, що миттєвий центр скоростей блока К знаходиться в точці 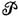, получимо: 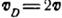. Так як мотузка ізрозтяжна, то швидкість груза В дорівнює швидкості точки D, тобто,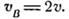

Миттєва кутова швидкість блока К: 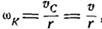, кутова швидкість блока L: 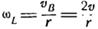,(швидкість точки на ободі блока L дорівнює швидкості блока В)

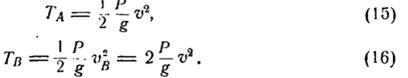Грузи А і В рухаються поступово, тому:

Блок К здійснює плоский рух, тобто

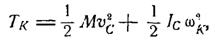
де 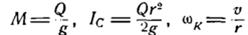. Тому:

Блок Lобертається навколо нерухомої осі, тоюто

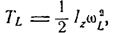
де 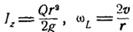. Виходячи з цього,

Підставивши вирази (15),(16),(17) і (18) в формулу (14) знаходимо кінетичну енергію системи

Відповідно умов задачі, швидкість груза А в початковому положенні системи дорівнювала 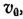, тобто

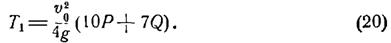
В кінцевому положенні системи швидкість груза А подвоїлась, відповідно

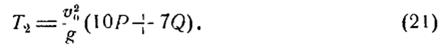
Підставивши формули (13),(20) і (21) у вираз (2) вирішивши цей приклад відносно s, визначимо переміщення груза А:

Підставивши вирази (15),(16),(17) і (18) в формулу (14) знаходимо кінетичну енергію системи

Використана література:

1. Аркуша А.И.Руководство к решению задач по теоретической механике. – М.: Высшая школа. – 1976. – 183 с.

2. Ердеді О.О., Аникін Ш.В., Медведєв Ю.О., Чуйков О.С. Технічна механіка. – К.: Вища школа – 1983. – 243 с.

3. Мовнин М.С., Израелит А.Б., Рубашкин А.Г. Основы технической механики. – Л.: Машиностроение. – 1990. – 205 с.

4. Павловский М.А. Теоретична механіка. – Київ: Техніка. – 2002. – 512 с.

5. Тарг С.М. Краткий курс теоретической механики. – М.: Высшая школа. – 2003. – 416 с.;

6. Мещерский И.В. Задачи по теоретической механике. – Санкт-Петербург: Лань. – 2001. – 448 с.

7. Яблонский А. А. Сборник заданий по теоретической механике. – М.: Интеграл-пресс. – 2006. – 382 с.

8. Яблонський А.А. Курс теоретической механики: В 2 т. М.: Высш. шк. – 2006. – Т.2. – 430 с.

9. Бугаєнко Г.О. Курс теоретичної механіки. – К., 1968. – 367 с.

10. Кильчевский Н.А., Ремизова Н.И., Кильчевская Е.Н. Основы теоретической механики.– К, 1986. – 295 с.

11. Кузьо І. В., Ванькович Т.-Н. М., Зінько Я. А., Смерека І. П.. Теоретична механіка. Кінематика.Навчальний посібник. Львів: Видавництво Львівської політехніки. – 2007. – 188 с.

12. Цасюк В.В. Теоретична механіка:Навчальний посібник. – К.:ЦУЛ, 2004. – 402 с.

Date: 2015-09-18; view: 328; Нарушение авторских прав