Теория Фрелиха и ее модификации

В теории диэлектрической поляризации Фрелиха (1960) выражение для проекции среднего электрического момента на направление макроскопического поля Е (М_Е)сферы объемом V, вырезанной в однородном и изотропном диэлектрике, имеет вид

,

где – статистический интеграл; q – угол между направлениями М и Е.

Внешняя по отношению к сфере часть диэлектрика считается сплошной средой с диэлектрической проницаемостью e_S, а макроскопическое (максвелловское) поле предполагается достаточно слабым.

При усреднении М_Е по всем направлениям (< cos ² q >=1/3) выражение для среднего значения электрического момента принимает вид

М_Е = , (61)

где М ² = J ^-1× 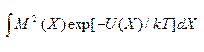– среднее значение квадрата электрического момента сферы в отсутствие электрического поля Е.

Согласно теории поляризации Фрелиха

М ² = Np²g_к, (62)

где р – дипольный момент молекулы в среде; N – число молекул в сфере; g_к – фактор Кирквуда. Из выражений (15), (61), (62) и Р = М_Е / V, получаем формулу

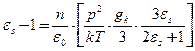, (63)

связывающую статическую диэлектрическую проницаемость вещества
с дипольным моментом отдельной молекулы в конденсированной среде
(n = N / V). Умножив (63) на молярный объем V ₀, получаем выражение для молярной поляризации конденсированного диэлектрика (N_A = nV ₀):

, (64)

Формула (63) представляет основной результат теории поляризации Фрелиха. Считается, что она получена достаточно строгим образом, однако для определения характеристик поляризации вещества она требует знания величин р и g_к.

Наряду с выражением (63) широко используются ее различные модификации. Наиболее известными из них являются модификации в виде формул Онзагера – Дюпюи (1962):

P_{M ор} = (e_S – e _¥) V ₀=(N_А / e ₀) × [ p ²/ kT)×(g_к / 3)] (64)

и Рахмана – Стиллинджера (1972)

P_M= (e_S – 1) V ₀=(N_А / e ₀)[ a× 3 e_S / (2 e_S + 1) + (p ²/ kT)× (g_к /3)×3 e_S (2 e_S + 1)]. (65)

В формулах (64) и (65), так же как и в формуле (63), дипольный момент молекулы в вакууме заменен на дипольный момент молекулы в среде. Замена m на p предполагает, что в электрическом поле ориентируется полный дипольный момент молекулы. Выражения в формулах (64) и (65), взятые в скобки, представляют собой соответственно ориентационную и общую поляризуемости молекулы, а их левые части – ориентационную и общую молярные поляризации. Полагая, что во льду Ih при температуре плавления р =9,740×10^-30 Кл×м (2,92 D), g_к =3,053 и e_¥=3,1, Негл (1973) получил e_S =92; это значение совпадает с экспериментальным. Нетрудно заметить, что выражение [a 3e _S (2e _S + 1)] в формуле (65) представляет собой деформационную поляризуемость молекулы. При a_эл =160,67×10^-42 Кл×м²×В^-1 (1,444×10^-24 см³) и e_S =92 значение деформационной поляризуемости молекулы воды во льду при температуре плавления равно 239,7×10^-42Кл×м²×В^-1 (2,154×10^-24 см³). Подставив это значение в формулу (66) (разновидность выражения (26))

(e_деф – 1) = (n / e ₀)× a _деф, (66)

при n =(N_A / V ₀)=3,06416 ×10^-28 м^-3 получаем, что значение e _деф (1,83) у льда Ih при температуре плавления практически равно внутренней составляющей высокочастотной диэлектрической проницаемости (формула (34)):

e _¥.внут=(n _эл. + D n _ат.)² =1,822.

По Рахману – Стиллинджеру (1972) во льду Ih при Т _плдипольный момент р =9,74×10^-30 Кл×м, фактор Кирквуда g_k ^* = и 2,07. Фактор Кирквуда по Рахману – Стиллинджеру отмечен нами как g_k ^*, так как это значение существенно отличается от 3. При р =9,74×10^-30 Кл, g_k ^*=2,07, V ₀=19,653×10^-6 м³×моль^-1, a _эл=160,67×10^-42 Кл×м²×В^-1 и e_S =92 левая часть формулы (2.6.9) равна 1 778, а правая – 1 788 м³×моль^-1.

Из формулы (65) следует, что a _деф= a _эл [3 e_S / (2 e_S + 1)], ориентационная и общая поляризуемости молекулы воды при Т _плсоответственно равны 239,7×10^-42, 25 907×10^-42Кл×м²×В^-1 (232,84×10^-24см³) и 26 147×10^-42 Кл×м²×В^-1 (235,00×10^-24 см³). Значения фактора Кирквуда по Неглу (g_к/ 3 =1,018) и по Рахману – Стиллинджеру (g_k ^*3 e_S / 3(2 e_S + 1)=1,029) при e_S =92 больше 1. Величина коэффициента локальной ориентационной упорядоченности, превышающая 1, по нашему мнению, физического смысла не имеет. Значения коэффициентов g_к / 3 и g_k^* [3 e_S / 3(2 e _S +1)] при температуре плавления льда больше 1, так как в формулах (64) и (65) занижены значения дипольного момента молекулы воды (в формуле (64) якобы определяется только ориентационная составляющая диэлектрической проницаемости; в формуле (65) величина дипольного момента уменьшена из-за разделения общей поляризуемости на деформационную и ориентационную).

Нетрудно заметить, что в большинстве работ по теории поляризации фактор Кирквуда входит в формулы в виде g_к / 3. Поэтому логично предположить, что значение максимума коэффициента локальной ориентационной упорядоченности диполей должно стремиться к 1. По мнению
Быкова (1993), мера локальной электрической упорядоченности диполей должна изменяться от 1 до 0 и представлять собой коэффициент
B = 1 – L ²(x). При больших значениях ориентирующего фактора х среднее значение косинуса угла между напряженностью внешнего поля и дипольными моментами р молекул воды в тонких пленках определяется из выражения (Антонченко, 1991):

á cosq ñ = cth (x) – (1 + e ^{-2 x} ) /x» cth (x)– (1/ x) = L (x).

У воды (даже в критическом состоянии) величина x существенно больше 1, поэтому á cosq ñ по своим значениям практически не отличается от функции Ланжевена. При замене g_k ^*3 e_S / 3(2 e_S + 1) на функцию g_к/ 3 и объединении деформационной и ориентационной поляризуемостей в общую поляризуемость выражения (64) и (65) принимают вид

Р_М = (e_S – 1) V ₀ = (N_А / e ₀)×(p ²/ kT)×(g_к /3). (67)

Последняя формула совпадает с формулой (49), полученной для вычисления диэлектрической проницаемости разреженных газов. Следовательно, форма зависимости статической диэлектрической проницаемости в виде уравнения (67) является общей для конденсированных и газообразных состояний вещества. При переходе от конденсированных состояний воды к разреженному газу значения e_S, р и g_к стремятся к соответствующим значениям этих характеристик в разреженных газах (e_S ® 1, р ® m, g_к ® 1).

Date: 2015-09-03; view: 916; Нарушение авторских прав