
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Способы задания движения точки
|
|
КИНЕМАТИКА
Студент должен:
Иметь представление:
- О пространстве, времени, траектории, пути, скорости, ускорении;
- О скоростях средней и истиной;
- Об ускорении при прямолинейном и криволинейном движениях;
- О различных видах движения точки;
- О поступательном движении, его особенностях и параметрах;
- О вращательном движении тела и его параметрах;
- О системах координат;
- Об абсолютном, относительном и переносном движениях;
- О плоскопараллельном движении
- О мгновенной оси вращения и мгновенном центре скоростей;
- О сложении двух вращательных движений
Знать:
- Формулы скоростей и ускорений точки (без вывода);
- Формулы (без вывода) и графики равномерного и равнопеременного движений точки;
- формулы для определения параметров поступательного и вращательного движения тела;
- Различные виды поступательного и вращательного движения твёрдого тела;
- Разложение сложного движения на переносное и относительное;
- Теорему сложения скоростей;
- Разложение плоскопараллельного движения на поступательное и вращательное;
- Способы определения положения мгновенного центра скоростей
Уметь:
- Способы задания и движения точки: естественный и координатный;
- Обозначение, единицы измерения, взаимосвязь кинематических параметров движения.
- Определять параметры движения точки;
- Строить и читать кинематические графики.
- Определять кинематические параметры тела при поступательном и вращательном движении;
- Определять параметры движения любой точки тела;
- Определять параметры движения материальной точки;
- Анализировать характер движения плоского механизма и его звеньев;
- Определять скорость любой точки плоского механизма.
Тема 1.7-1.8 Основные понятия кинематики. Кинематика точки
Кинематика - часть теоретической механики, изучающая общие законы движения материальных точек и твердых тел без учета причин, вызывающих эти движения.
Кинематика отвечает на вопрос: как движется тело.
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
- Характеристики движения
Любое механическое движение характеризует следующие параметры:
- траектория движения;
- путь;
- перемещение;
- скорость;
- ускорение
Траектория движения — это линия, вдоль которой движется тело. В зависимости от траектории движение может быть прямолинейным и криволинейным.
Путь s — это расстояние, пройденное телом вдоль линии траектории
(рис. 1.40).
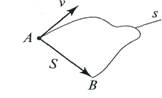
Рис. 1.40
Перемещение S - это направленный отрезок прямой, соединяющий начальное и конечное положение тела (см. рис. 1.40).
Скорость v — кинематическая мера движения точки, характеризующая быстроту изменения её положения в пространстве:
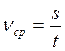 ; м/с
; м/с
Истинная скорость при любом движении точки равна первой производной координаты (т.е. расстояния от начала отсчёта перемещения) по времени.
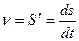 ,м/с,
,м/с,
Скорость векторная величина, которая направлена по касательной к траектории в сторону движения.

Ускорение точки а - кинематическая мера изменения вектора скорости точки по величине и направлению в единицу времени.
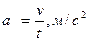
Истинное ускорение при любом движении точки равно первой производной скорости или второй производной координаты (т.е. расстояния от начала отсчёта перемещения) по времени.
 ; [а]=[S]/[t]2=м/с2
; [а]=[S]/[t]2=м/с2
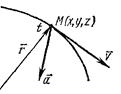
При прямолинейном движении вектор ускорения совпадает с траекторией, при криволинейном движении он направлен в сторону вогнутости траектории.
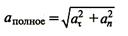
|
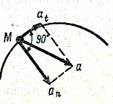
В криволинейном движении ускорение зависит от кривизны траектории. Чтобы определить величину и направление истинного полного ускорения точки а его необходимо разложить на две перпендикулярные составляющие: 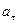 касательное (тангенциальное) и
касательное (тангенциальное) и 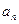 нормальное (центростремительное)ускорения.
нормальное (центростремительное)ускорения.
|
Касательное ускорение 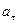 — это величина, которая характеризует быстроту изменения величины скорости за единицу времени:
— это величина, которая характеризует быстроту изменения величины скорости за единицу времени:
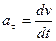 ,м/с2,
,м/с2, 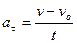 .
.
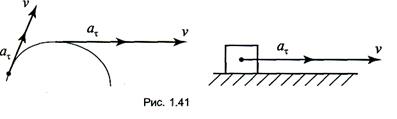
Касательное ускорение всегда направлено по линии вектора скорости (рис. 1.41).
|
Нормальное ускорение 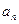 — это величина, которая характеризует изменение направления вектора скорости:
— это величина, которая характеризует изменение направления вектора скорости:

где r— радиус кривизны траектории.
Нормальное ускорение всегда направлено по радиусу к центру кривизны траектории (рис. 1.42).
Способы задания движения точки.
Чтобы задать движение точки, необходимо, указать её положение в пространстве по отношению к выбранной системе отсчёта в любой момент времени.
Рассмотрим 2 способа задания движения точки: естественный и координатный.
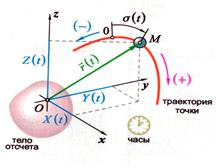
Естественный способ заключается в том, что движение точки задаётся её траекторией, началом отсчёта и уравнением движения (законом движения) по этой траектории.
Уравнение движения – это уравнение, определяющее положение движущейся точки в зависимости от времени.

|
О – начало отсчёта
S –дуговая координата – это расстояние на траектории между точкой и началом отсчета, отсчитываемое в соответствии с правилом знаков;
S=f(t)- уравнение или закон движения точки:
где: S- дуговая координата, является функцией времени;
t- время движения точки в начальный момент времени.
Дуговую координату не следует путать с длиной пройденного пути. Путь с течением времени увеличивается, а координата устанавливает положение движущейся точки относительно начала отсчета.
Зная траекторию точки и уравнение движения по этой траектории, можно определить положение точки в любой момент времени,подставив время в уравнение движения.
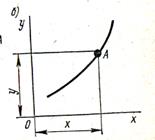 Координатный способ заключается в том, что движение точки задаётся движением её координат x и y, которыеизменяются с течением времени, значит являются некоторыми функциями времени.
Координатный способ заключается в том, что движение точки задаётся движением её координат x и y, которыеизменяются с течением времени, значит являются некоторыми функциями времени.
x=f1(t),
- Уравнения плоского движения точки в координатной
y=f2(t) форме
Зная уравнения движения точки в координатной форме, можно, подставив в эти уравнения время, определить положение проекции точки, а значит положение самой точки в любой момент времени.
Чтобы определить уравнение траектории движения точки, необходимо решить эти уравнения, исключив из них параметр время.
y=f(x)- Уравнение траектории
Пример 1 При движении точки её координаты изменяются с течением времени и определяются уравнениями:
1) x = f1(t) = 8 t +20 мм
2) y = f2(t) = 5 t мм
Найти уравнение траектории движения точки.
Решение
Из уравнения (2) находим
t = y /5= 0,2 y
Подставляем t в (1) уравнение и получим уравнение траектории
x =8 t + 20 = 8• 0,2 y +20 = 1,6 y +20 мм
x =1,6 y +20 мм - уравнение траектории
Ответ: Уравнение показывает, что траектория движения точки представляет собой прямую линию.
Date: 2015-09-03; view: 1011; Нарушение авторских прав