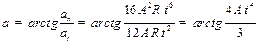Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Угловая скорость
|
|
Угловой скоростью вращения абсолютно твердого тела называется вектор 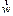 , численно равный производной от угла поворота по времени и направленный вдоль оси вращения таким образом, чтобы он совпадал по направлению с поступательным движением правого винта, который вращается вместе с телом:
, численно равный производной от угла поворота по времени и направленный вдоль оси вращения таким образом, чтобы он совпадал по направлению с поступательным движением правого винта, который вращается вместе с телом:
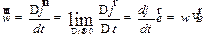
| (1.20) |
Единица измерения угловой скорости - 1рад/с.

| Здесь  - радиус – вектор, проведенный от центра вращения к точке, для которой определяется линейная скорость.
Наряду с угловой скоростью вращения тела пользуются понятиями периода и частоты вращения.
Периодом - радиус – вектор, проведенный от центра вращения к точке, для которой определяется линейная скорость.
Наряду с угловой скоростью вращения тела пользуются понятиями периода и частоты вращения.
Периодом  вращения называется промежуток времени, в течение которого тело, вращаясь с угловой скоростью w, совершает один полный оборот. вращения называется промежуток времени, в течение которого тело, вращаясь с угловой скоростью w, совершает один полный оборот.
|
| Рисунок 1.9. |
Частотой вращения  называется число оборотов, совершаемых телом за 1 секунду при равномерном вращении с угловой скоростью w.
называется число оборотов, совершаемых телом за 1 секунду при равномерном вращении с угловой скоростью w.
По определениям:
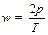 , , 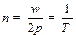
| (1.21) |
Отметим, что при равномерном вращении (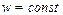 ) угловая скорость w может называться циклической или круговой частотой.
) угловая скорость w может называться циклической или круговой частотой.
По аналогии с () введем понятие средней угловой скорости. Средней угловой скоростью 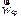 называется отношение:
называется отношение:
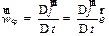
| (1.22) |
Средняя угловая скорость 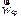 направлена так же, как и вектор
направлена так же, как и вектор  углового перемещения.
углового перемещения.
1. 2. 3. Угловое ускорение.
Для характеристики быстроты изменения вектора угловой скорости  при неравномерном вращательном движении твердого тела вокруг неподвижной оси (или точки) вводится понятие вектора углового ускорения.
при неравномерном вращательном движении твердого тела вокруг неподвижной оси (или точки) вводится понятие вектора углового ускорения.
Угловым ускорением называется вектор 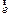 равный производной по времени от угловой скорости или второй производной от угла поворота:
равный производной по времени от угловой скорости или второй производной от угла поворота:

| (1.23) |
Единица измерения углового ускорения - 1рад/с2.
При вращении тела вокруг неподвижной оси изменения вектора 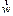 обусловлены изменениями его численного значения.
обусловлены изменениями его численного значения.
Вектор 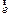 направлен вдоль оси вращения, в ту же сторону что и вектор
направлен вдоль оси вращения, в ту же сторону что и вектор 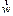 при
при 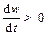 (при равноускоренном движении) и при
(при равноускоренном движении) и при  – в противоположную сторону (при равнозамедленном движении).
– в противоположную сторону (при равнозамедленном движении).
1. 3. Связь линейных и угловых кинематических величин.
Рассмотрим произвольную точку М твердого тела, вращающегося вокруг неподвижной оси OZ с угловой скоростью  , которая описывает окружность радиуса R с центром в точке О¢. (Рис. 1.10).
, которая описывает окружность радиуса R с центром в точке О¢. (Рис. 1.10).
Вектор линейной скорости 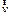 (и перемещения
(и перемещения 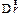 ) точки M лежит в плоскости перпендикулярной оси вращения OZ и перпендикулярен вектору вектору угловой скорости
) точки M лежит в плоскости перпендикулярной оси вращения OZ и перпендикулярен вектору вектору угловой скорости  (и углового перемещения
(и углового перемещения  ) и радиус-
) и радиус-
 
| вектору  .
Тогда .
Тогда

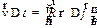 
|
| Рисунок 1.10. |
Следовательно,
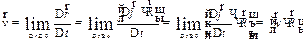
| (1.24) |
Т.к. 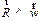 , то в скалярной форме:
, то в скалярной форме:

| (1.25) |
Полученное выражение (1.24) носит название формулы Эйлера. Для ускорения получаем:
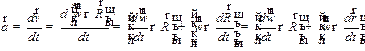
|
Учтем, что
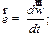 и и 
|
и окончательно получим:
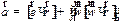
| (1.26) |
Первый член в правой части полученного выражения представляет собой рассмотренное ранее тангенциальное ускорение:
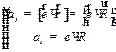
| (1.27) |
Второй член в правой части, учитывая (1.24), преобразуем к виду:
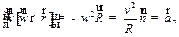 , ,
| (1.28) |
т.е. он представляет собой нормальное ускорение.
| Пример. |
Решение: Имеем по определениям угловой скорости и углового ускорения
По формулам (1.27) и (1.28) находим
По формуле (1.18) находим
Угол равен арктангенсу отношения нормального и тангенциального отношения (с точностью до
|
1. 4. Преобразование координат, скоростей и ускорений при переходе из одной системы отсчета в другую.
Пусть движение точки 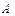 в системе отсчета
в системе отсчета 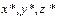 задано законом
задано законом 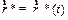 . При этом система отсчета
. При этом система отсчета 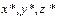 совершает относительно неподвижного наблюдателя сложное движение. Ставится задача о связи кинематических характеристиках движения этой точки в системах отсчета
совершает относительно неподвижного наблюдателя сложное движение. Ставится задача о связи кинематических характеристиках движения этой точки в системах отсчета 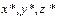 и
и 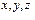 , которая неподвижна относительно наблюдателя. Представим это сложное движение системы как сумму поступательного движения системы
, которая неподвижна относительно наблюдателя. Представим это сложное движение системы как сумму поступательного движения системы 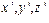 относительно
относительно 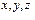 и вращения системы
и вращения системы 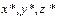 относительно
относительно 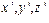 с угловой скоростью
с угловой скоростью 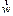 (см. рис.1.11).
(см. рис.1.11).
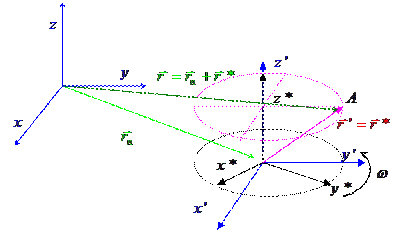 
|
| Рисунок 1.11. |
Тогда имеем уравнение
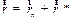
| (1.29) |
где  - радиус-вектор точки
- радиус-вектор точки  с системе
с системе  ,
, 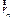 - радиус-вектор начала отсчета системы
- радиус-вектор начала отсчета системы 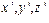 в
в 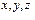 ,
, 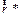 =
= 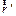 - радиус-вектор точки
- радиус-вектор точки 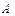 с системе
с системе 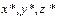 (или
(или 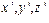 , т.к. в системах
, т.к. в системах 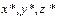 и
и 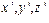 - радиус-векторы точки
- радиус-векторы точки 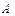 [
[ 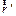 и
и 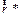 соответственно] совпадают).
соответственно] совпадают).
Найдем связь (преобразование) скоростей и ускорений точки в этих системах. Для установления преобразования скоростей дифференцируем (1.29). Имеем:
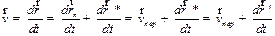
| (1.30) |
где 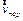 - скорость начала координат системы отсчета
- скорость начала координат системы отсчета 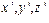 в системе
в системе 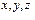 или переносная скорость,
или переносная скорость, 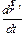 - скорость точки в системе
- скорость точки в системе 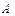 отсчета
отсчета 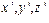 или относительная скорость (для неподвижного наблюдателя).
или относительная скорость (для неподвижного наблюдателя).
Аналогично для ускорений получаем
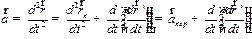
| (1.31) |
где  - ускорение начала координат системы отсчета
- ускорение начала координат системы отсчета 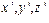 в системе
в системе 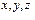 или переносное ускорение,
или переносное ускорение,  - ускорение точки С в системе отсчета
- ускорение точки С в системе отсчета 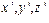 или относительное ускорение (для неподвижного наблюдателя).
или относительное ускорение (для неподвижного наблюдателя).
Найдем 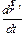 и
и  . Для этого несколько упростим задачу: будем
. Для этого несколько упростим задачу: будем

| считать, что система отсчета 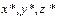 вращается в неподвижной системе отсчета вращается в неподвижной системе отсчета 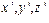 (см. рис. 1.12) вокруг совпадающих осей (см. рис. 1.12) вокруг совпадающих осей 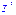 и и 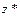 .
Отметим, что согласно постулатам (аксиомам) классической физики расстояние между точками и временные интервалы между событиями в .
Отметим, что согласно постулатам (аксиомам) классической физики расстояние между точками и временные интервалы между событиями в
|
| Рисунок 1.12. |
различных системах отсчета одинаковы.
Следовательно, изменение радиус-векторов точки 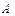 в указанных системах отсчета
в указанных системах отсчета 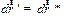 . Но, изменение вектора
. Но, изменение вектора  есть только произведение скорости
есть только произведение скорости  точки
точки 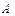 в системе отсчета
в системе отсчета 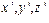 на промежуток времени
на промежуток времени 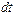 , а изменение вектора
, а изменение вектора 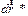 есть результат перемещения
есть результат перемещения  точки
точки 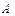 системе отсчета
системе отсчета 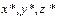 и поворота вектора
и поворота вектора 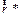 на угол
на угол 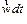 , т. е.
, т. е.
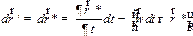
| (1.32) |
Следовательно, скорости точки 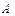 в этих системах отсчета связаны соотношением
в этих системах отсчета связаны соотношением
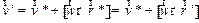
| (1.33) |
Отметим, что в этом случае 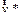 - есть относительная, а
- есть относительная, а 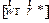 переносная скорости.
переносная скорости.
Найдем изменение скорости  точки
точки 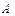 в системе отсчета
в системе отсчета 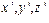 за промежуток времени
за промежуток времени 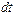 :
:
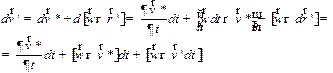
| (1.34) |
Тогда для ускорений получаем

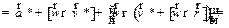
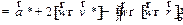
| (1.35) |
Заметим, что векторное произведение 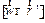 остается неизменным и по величине и по направлению для всех векторов
остается неизменным и по величине и по направлению для всех векторов 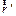 , начала которых лежат на оси вращения. Удобно ввести вектор
, начала которых лежат на оси вращения. Удобно ввести вектор 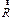 , направление которого перпендикулярно оси вращения. Тогда
, направление которого перпендикулярно оси вращения. Тогда 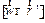 =
= 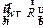 и
и 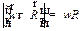 .
.
Следовательно, 
Поэтому выражение (1.35) примет вид
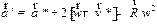 , ,
| (1.36) |
а выражение (1.31) запишем так
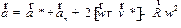 , ,
| (1.37) |
Раскроем смысл входящих сюда величин. 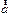 - ускорение тела относительно неподвижного наблюдателя, с которым связана система отсчета
- ускорение тела относительно неподвижного наблюдателя, с которым связана система отсчета 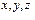 ,
,  - ускорение тела в системе отсчета
- ускорение тела в системе отсчета 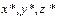 ,
, 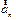 - ускорение начала координат системы отсчета
- ускорение начала координат системы отсчета 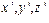 , движущейся поступательно относительно
, движущейся поступательно относительно 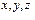 ,
,  - так называемое центростремительное ускорение и, наконец,
- так называемое центростремительное ускорение и, наконец,  - кориолисово или поворотное ускорение.
- кориолисово или поворотное ускорение.
Итак, кинематические величины тела в вышеупомянутых системах отсчета связаны следующим образом
| Система отсчета | Радиус-вектор | скорость | ускорение |
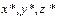
| 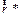
| 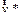
| 
|
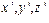
| 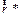 = = 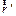
| 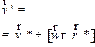
| 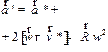
|
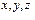
| 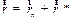
| 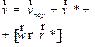
| 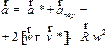
|
Вопросы для самоконтроля.
1. Что изучается в разделе "Кинематика"?
2. Дайте определение механического движения.
3. Какое движение называется поступательным?
4. Что такое система отсчета?
5. Что такое вектор перемещения?
6. Что такое траектория? Виды траекторий, относительность понятия траектории.
7. Дайте определение пути.
8. В чем заключается закон независимости движений?
9. Какое движение называют равномерным, неравномерным, равнопеременным?
10. Дайте определение средней и мгновенной скоростей неравномерного движения.
11. Ускорение при криволинейном движении, его нормальная и тангенциальная составляющие.
12. Виды движения материальной точки.
13. Что называют абсолютно твердым телом?
14. Дайте определение вращательного движения.
15. Что называют угловой скоростью? Ее направление, единицы измерения угловой скорости.
16. Какая связь между линейной и угловой скоростями?
17. Дайте определение периода и частоты обращения. Связь между ними.
18. Что называют угловым ускорением? Его направление. Единицы измерения углового ускорения.
19. Какая существует аналитическая связь между линейными и угловыми величинами?
Задачи для самостоятельного решения
1.8; 1.15; 1.22; 1.36; 1.39; 1.47;1.60 [3] или 1.10; 1.16; 1.28; 1.33; 1.40; 1.53; 1.58; [4].
Литература
1. Савельев И.В. Курс общей физики, т.1.-М.:"Наука",-1977.-416с. (§1-4 и §6-17)
2. Трофимова Т.И. Курс физики.-М.:"Высш.шк.",-1985.-432с. (§1-3 и §5-8)
3. Волькенштейн В.С. Сб. задач по общему курсу физики.-М.: "Наука",-1985.-382 с.
4. Чертов А.Г., Воробьёв А.А. Задачник по физике.-М.: "Высш.шк.",-1981.-496с.
Date: 2015-09-03; view: 1332; Нарушение авторских прав
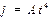 . Найти угловое, нормальное, тангенциальное и полное ускорение точки диска, расположенной на расстоянии R от оси вращения, а также угол
. Найти угловое, нормальное, тангенциальное и полное ускорение точки диска, расположенной на расстоянии R от оси вращения, а также угол 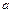 между вектором скорости и полного ускорения.
между вектором скорости и полного ускорения.
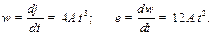
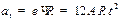 ,
, 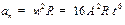
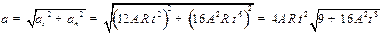
 )
)