
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определим ускорение произвольно движущейся точки
|
|
В общем случае траектория точки представляет из себя пространственную кривую. Введем следующие понятия:
Соприкасающейся плоскостью в точке М траектории называется предельное положение плоскости, проходящей через любые три точки траектории, когда эти точки неограниченно приближаются к точке М.
Соприкасающейся окружностью в точке M траектории называется предельная окружность, полученная из произвольной окружности проходящей через три точки траектории при их неограниченном приближении к точке М.
Соприкасающаяся окружность лежит в соприкасающейся плоскости.
Центр соприкасающейся окружность и ее радиус называются соответственно центром кривизны и радиусом кривизны рассматриваемой кривой в точке М.
Прямая, соединяющая точку М с центром кривизны называется главной нормалью к кривой в точке М.
 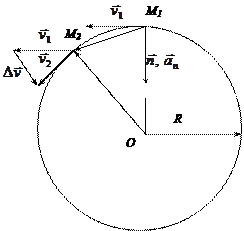
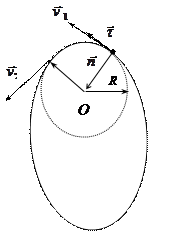
| Cначала найдем ускорение точки равномерно перемещающейся по окружности радиуса 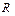 (см. рис. 1.3). Скорость (см. рис. 1.3). Скорость 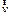 направлена по касательной к окружности. Для двух положений точки: M1 в момент времени t и M2 в момент времени t + ∆t имеем векторы скоростей направлена по касательной к окружности. Для двух положений точки: M1 в момент времени t и M2 в момент времени t + ∆t имеем векторы скоростей 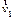 и и 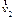 соответственно. Из рис. 1.3 видно, что треугольник, образованный этими векторами и вектором изменения скорости соответственно. Из рис. 1.3 видно, что треугольник, образованный этими векторами и вектором изменения скорости 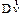 , и равнобедренный треугольник с боковыми сторонами, равными радиусу , и равнобедренный треугольник с боковыми сторонами, равными радиусу 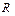
|
| Рисунок 1.3. |
окружности и перемещение точки подобны. Следовательно,

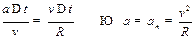
Ускорение 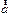 может быть представлено в виде:
может быть представлено в виде:
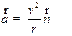 , ,
| (1.13) |
где 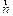 - единичный вектор нормали к круговой траектории движения точки (направлен к центру кривизны траектории).
- единичный вектор нормали к круговой траектории движения точки (направлен к центру кривизны траектории).
Представим вектор скорости в виде:
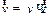
| (1.14) |
где  - единичный вектор, направленный по касательной к окружности и указывающий направление скорости,
- единичный вектор, направленный по касательной к окружности и указывающий направление скорости, 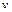 – величина скорости, т.е. ее численное значение.
– величина скорости, т.е. ее численное значение.
При равномерном движении модуль скорости равен константе (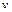 = const), меняется только направление вектора касательной. Тогда для такого случая:
= const), меняется только направление вектора касательной. Тогда для такого случая:
 . .
| (1.15) |
Сравниваем с формулой ускорения через 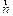 (1), получим:
(1), получим:
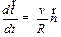 . .
| (1.16) | |
| При равномерном движении ускорение 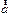 направлено к центру, т.е. перпендикуляр траектории, но не так будет обстоять дело, когда скорость направлено к центру, т.е. перпендикуляр траектории, но не так будет обстоять дело, когда скорость 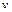 ¹ const. В общем случае произвольной гладкой кривой радиус кривизны меняется от точки к точке (см., например, рис. 1.4). Непрерывно меняется и направление единичного вектора главной нормали ¹ const. В общем случае произвольной гладкой кривой радиус кривизны меняется от точки к точке (см., например, рис. 1.4). Непрерывно меняется и направление единичного вектора главной нормали 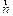 .
Рассмотрим этот случай.
Имеем .
Рассмотрим этот случай.
Имеем
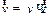 тогда
тогда
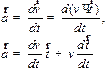
| |
| Рисунок 1.4. | ||
Применяем подстановку, исходя из формул (1.13) и (1.15) получаем:
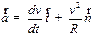
| (1.17) |
Заменим 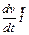 на
на 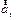 (тангенциальное ускорение), а
(тангенциальное ускорение), а 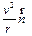 на
на 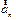 (нормальное ускорение), получим
(нормальное ускорение), получим
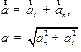 . .
| (1.18) |
Тангенциальное ускорение 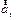 меняет скорость по величине, нормальное ускорение
меняет скорость по величине, нормальное ускорение 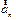 меняет скорость по направлению.
меняет скорость по направлению.
Действительно, если дана некая траектория (см. рис. 1.5) есть скорость 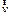 в начале и скорость
в начале и скорость 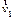 во втором положении, перенесем параллельным переносом вектор
во втором положении, перенесем параллельным переносом вектор 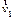 в точку M 1, тогда мы видим, что вектор скорости получает приращение
в точку M 1, тогда мы видим, что вектор скорости получает приращение 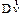 .
.
В результате, если уменьшать промежутки времени D t к нулю, то оба соотношения (см. рис. 1.6) 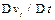 и
и  будут стремиться к пределам
будут стремиться к пределам
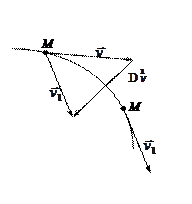
| 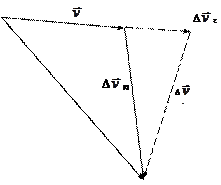
| |
| Рисунок 1.5. | Рисунок 1.6. |
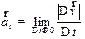 и
и 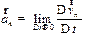 .
.
| Пример. | 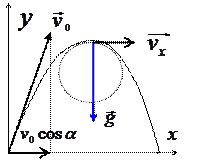
| Пример: Снаряд выпущен с начальной скоростью V = 200 м/с под углом a = 60° к горизонту. Определить кривизну траектории в точке наивысшего подъема снаряда (Рис.1.7). Силами аэродинамического сопротивления пренебречь. |
| Рисунок 1.7. | Решение:
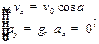
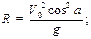
| |
В верхней точке
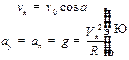
|
1. 2. КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Абсолютно твердое тело есть такое тело, в котором расстояние между любыми двумя частями которого остается неизменным. (Напомним, что абсолютно жесткой геометрической фигурой является треугольник).
Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая жестко связанная с телом перемещается параллельно самой себе (см. рис. 1.8).
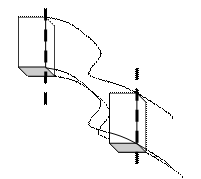
| Все точки тела движущегося поступательно в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе, поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся тело обладает тремя степенями свободы. |
| Рисунок 1.8. |
Теперь можно уточнить границы применимости модели материальной точки. Модель материальной точки применима только к телу, движущемуся поступательно.
Вывод: описание поступательного движения тела есть описание движения материальной точки.
Твердое тело, свободно движущееся в пространстве, имеет три степенипоступательного движения, соответствующие возможности его перемещения вдоль трех осей координат.
1. 2. 1. Вращательное движение твердого тела вокруг неподвижной оси.
При вращении или вращательном движении твердого тела вокруг неподвижной оси все его точки тела описывают окружности, центры которых лежат на прямой, называемой осью вращения, а плоскости окружностей перпендикулярны ей. Тело, вращающееся вокруг неподвижной оси 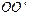 , обладает одной степенью свободы (например, диск на рис. 1.9). Его положение определяется заданием угла j поворота от некоторого начального положения, т.к. все точки совершают за любой промежуток времени одинаковые угловые перемещения. В общем случае положение (ориентацию) тела в пространстве можно описать с помощью угловых координат (углов Эйлера).
, обладает одной степенью свободы (например, диск на рис. 1.9). Его положение определяется заданием угла j поворота от некоторого начального положения, т.к. все точки совершают за любой промежуток времени одинаковые угловые перемещения. В общем случае положение (ориентацию) тела в пространстве можно описать с помощью угловых координат (углов Эйлера).
Введем векторную величину 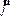 , характеризующую положение (ориентацию) тела в пространстве с помощью угла относительно некоторой точки:
, характеризующую положение (ориентацию) тела в пространстве с помощью угла относительно некоторой точки:
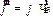
| (1.19) |
где 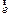 - единичный вектор, направление которого определяется по правилу буравчика (правого винта). Тогда изменение положения тела при вращении можно описать с помощью углового перемещения
- единичный вектор, направление которого определяется по правилу буравчика (правого винта). Тогда изменение положения тела при вращении можно описать с помощью углового перемещения 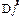 , равного по величине углу поворота
, равного по величине углу поворота 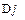 .
.
Единица измерения угла - 1рад. (Напомним, что радиан является естественной мерой угла. По определению центральный угол, охватывающий дугу, длина которой равна радиусу окружности, равен 1 радиану).
Date: 2015-09-03; view: 840; Нарушение авторских прав