Скорость, мгновенная и средняя скорость. Средняя путевая скорость

Быстрота перемещения тела в пространстве характеризуется скоростью.

В случае равномерного движения величина скорости 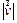, которой обладает частица в каждый момент времени, можно вычислить, разделив путь (S) на время (t).

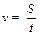
Рассмотрим теперь случай неравномерного движения. Разобьем траекторию (см. рис. 1.2) на бесконечно малые участки длины D S.

Каждому из участков сопоставим бесконечно малое приращение 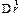. Пусть в момент времени t материальная точка M находится в положении, которое описывается радиус-вектором .

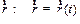Спустя некоторое время D t она переместится в M ₁ с радиус-вектором .

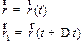
	Радиус-вектор мате­ри­альной точки получит приращение: 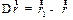    Разделив это переме­щение 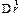на соот­ветствующий проме­жуток времени
Рисунок 1.2.

D t получим среднюю скорость.

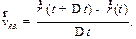
(1.3)

Если брать все меньшие промежутки D t, устремляя их к нулю, тогда соотношение на D t в пределе даст значение скорости в момент времени t.

Эта скорость называется истинной или мгновенной скоростью материальной точки в момент времени t, и определяется выражением:

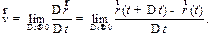
(1.4)

Т.к. 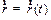– есть функция, то по определению производной

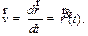
(1.5)

Средней путевой скоростью называется скалярная величина, равная отношению длины ∆S участка траектории к продолжительности ∆t прохождения его точкой: .

При криволинейном движении . Поэтому в общем случае средняя путевая скорость не равна модулю средней скорости 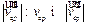. Здесь знак равенства соответствует прямолинейному участку траектории.

Единица измерения скорости - 1 м/с.

Разложение вектора скорости 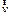по базису прямоугольной декартовой системы координат имеет вид:

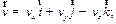
(1.6)

Проекции скорости точки на оси координат равны первым производным по времени от соответствующих координат точки:

,

(1.7)

а модуль вектора скорости:

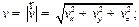
(1.8)

Пример

Пример: Материальная точка движется по закону 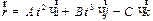. Определить закон изменения ее скорости. Решение: Имеем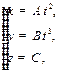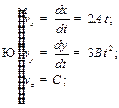

Date: 2015-09-03; view: 665; Нарушение авторских прав