Кинематика материальной точки

2.1. Кинематические уравнения движения

материальной точки

2.2. Скорость и ускорение материальной точки

2.1. Движение материальной точки может быть описано тремя способами: векторным, координатным и естественным. Этим трем способам описания соответствуют три вида кинематических уравнений движения:

– кинематическое уравнение движения в векторной форме:

,

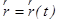где 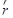– радиус-вектор материальной точки;

– кинематические уравнения движения в коорди натной форме, которые в неподвижной декартовой системе координат имеют вид:

.

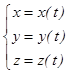Рис. 1

Естественный способ описания движения применяют в том случае, когда задано уравнение траектории материальной точки. На траектории выбирают начало отсчета. Расстояние, измеренное вдоль траектории от начала отсчета до положения, занимаемого материальной точкой в некоторый момент времени, называют пройденным путем 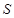(рис. 1). Кинематическое уравнение движения при таком способе описания при заданном уравнении траектории будет иметь вид: .

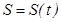2.2.Скорость – это векторная величина, которая характеризует быстроту изменения положения материальной точки в пространстве и направление её движения в каждый момент времени:

.

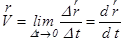Радиус-вектор материальной точки можно записать в виде

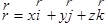(2.1)

С учетом выражения (2.1) для скорости получаем:

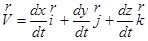, (2.2)

т.е.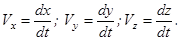

Модуль скорости может быть тогда определен как:

.

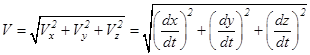При естественном способе описания движения

.

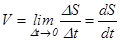С учетом того, что скорость направлена по касательной к траектории в каждой ее точке, будем иметь

,

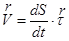где 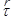– тангенциальный вектор, модуль которого равен единице, и который направлен по касательной к траектории в каждой её точке.

Ускорение – это векторная величина, которая характеризует быстроту изменения скорости:

.

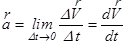С учетом (2.1) и (2.2) можно записать:

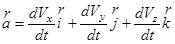
или

.

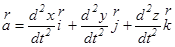Модуль ускорения может быть найден из выражения:

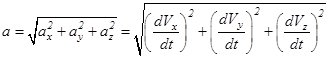
или

.

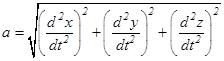При естественном способе описания движения ускорение представляют как сумму тангенциального ускорения 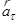, направленного по касательной к траектории движения в данной точке, и нормального (центростремительного) ускорения 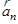, направленного по нормали к касательной к центру кривизны траектории в данной точке:

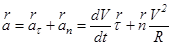. (2.3)

Модуль тангенциального ускорения характеризует изменение величины (абсолютного значения) скорости. Модуль нормального ускорения характеризует изменение направления скорости.

Date: 2015-09-03; view: 417; Нарушение авторских прав