
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача К3
|
|
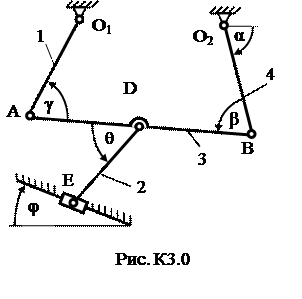
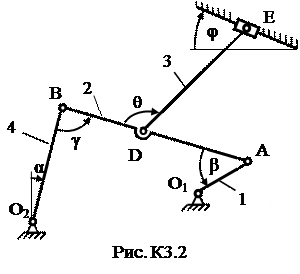
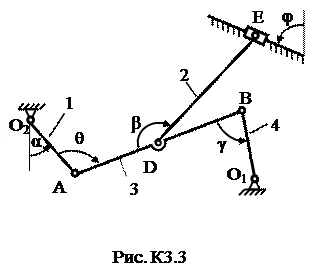
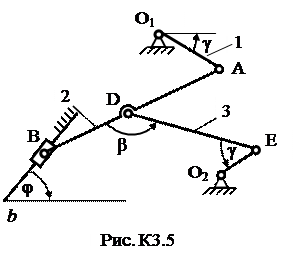
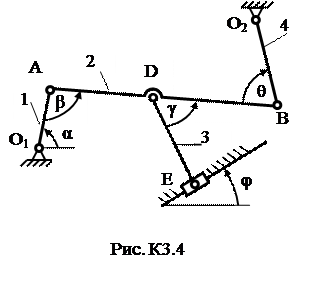
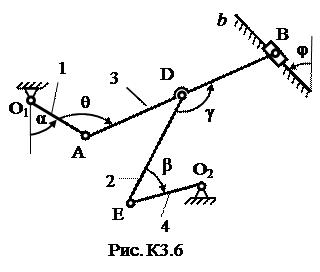
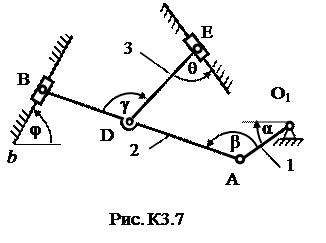
Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е (рис. К3.0 – К3.7) или из стержней 1, 2, 3 и ползунов В и Е (рис. К3.8, К3.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; т. D находится в середине стержня АВ. Длина стержней: l 1 = 0,4 м; l 2 = 1,2 м; l 3 = 1,4 м; l 4 = 0,6 м. Положение механизма определяется углами α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0−4) или в табл. К3б (для рис. 5−9); при этом в табл. К3а ω1 и ω4 – величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол γ на рис. 8 следует отложить от DE против хода часовой стрелки, а на рис. 9 – по ходу часовой стрелки и т.д.). Построение чертежа начинать со стержня, направление которого определяется углом α; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3б). Заданные угловую скорость и угловое ускорение считать направленными против хода часовой стрелки, а заданные скорость 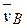 и ускорение
и ускорение 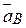 - от т. В к т. b (рис. К3.5−К3.9).
- от т. В к т. b (рис. К3.5−К3.9).
Указания. Задача К3 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности. При определении ускорений точек механизма исходить из векторного равенства  , где А – точка, ускорение
, где А – точка, ускорение 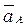 которой или задано, или непосредственно определяется по условиям задачи (если т. А движется по дуге окружности, то
которой или задано, или непосредственно определяется по условиям задачи (если т. А движется по дуге окружности, то 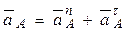 ; В – точка, ускорение
; В – точка, ускорение 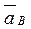 которой нужно определить (если т. В движется по дуге окружности радиуса l, то
которой нужно определить (если т. В движется по дуге окружности радиуса l, то  , где численно
, где численно 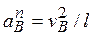 ; входящая сюда скорость v B определяется так же, как и скорости других точек механизма).
; входящая сюда скорость v B определяется так же, как и скорости других точек механизма).
Таблица К3а (к рис. К3.0 – К3.4)
| Номер условия | Углы, град | Дано | Найти | ||||||||
| α | β | γ | φ | θ | ω1, 1/с | ω4, 1/с | υ точек | ω звена | a точки | ε звена | |
| - | B, E | DE | B | AB | |||||||
| - | A, E | AB | A | AB | |||||||
| - | B, E | AB | B | AB | |||||||
| - | A, E | DE | A | AB | |||||||
| - | D, E | AB | B | AB | |||||||
| - | A, E | AB | A | AB | |||||||
| - | B, E | DE | B | AB | |||||||
| - | A, E | DE | A | AB | |||||||
| - | D, E | AB | B | AB | |||||||
| - | A, E | DE | A | AB |
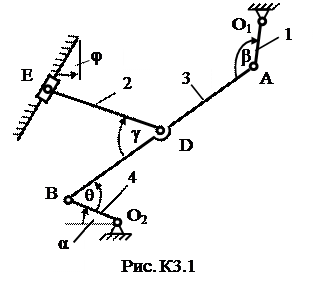
Таблица К3б (к рис. К3.5 – К3.9)
| Номер условия | Углы, град | Дано | Найти | ||||||||||
| α | β | γ | φ | θ | ω1, 1/с | ε1, 1/с2 | υВ, м/с | αВ, м/с2 | v точек | ω звена | a точки | ε звена | |
| - | - | B, E | AB | B | AB | ||||||||
| - | - | A,E | DE | A | AB | ||||||||
| - | - | B, E | AB | B | AB | ||||||||
| - | - | A,E | AB | A | AB | ||||||||
| - | - | B, E | DE | B | AB | ||||||||
| - | - | D,E | DE | A | AB | ||||||||
| - | - | B, E | DE | B | AB | ||||||||
| - | - | A,E | AB | A | AB | ||||||||
| - | - | B, E | DE | B | AB | ||||||||
| - | - | D,E | AB | A | AB |

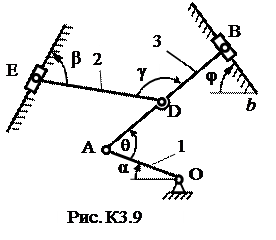
Пример К3. Механизм (рис. К3а) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами.
Дано: a=60º; b=150º; g=90º; j=30º; q=30º; AD = DB; l 1 = 0,4 м; l 2 = 1,2 м; l 3 = 1,4 м; w1 = 2 с-1; e1 = 7 с-2 (направление w1 и e1 – против хода часовой стрелки). Определить: v B, v E, w2, a B, e3.
Решение
1. Строим положение механизма в соответствии с заданными углами (рис. К3б).
2. Определяем v В. Т. В принадлежит стержню АВ. Чтобы найти v В, надо знать скорость какой-нибудь другой точки этого стержня и направление 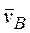 . По данным задачи, учитывая направление w1, можем определить
. По данным задачи, учитывая направление w1, можем определить 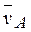 ; численно
; численно
 (1)
(1)
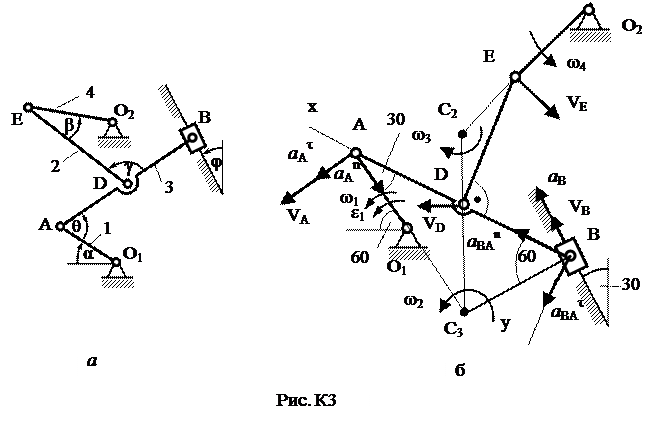
Направление  найдем, учтя, что т. В принадлежит звену АВ и одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная
найдем, учтя, что т. В принадлежит звену АВ и одновременно ползуну, движущемуся вдоль направляющих поступательно. Теперь, зная 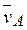 и направление
и направление 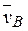 , воспользуемся теоремой о проекциях скоростей двух точек на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор
, воспользуемся теоремой о проекциях скоростей двух точек на прямую, соединяющую эти точки (прямая АВ). Сначала по этой теореме устанавливаем, в какую сторону направлен вектор 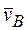 (проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
(проекции скоростей должны иметь одинаковые знаки). Затем, вычисляя эти проекции, находим
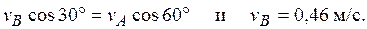 (2)
(2)
3. Определяем  . Т. Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить
. Т. Е принадлежит стержню DE. Следовательно, по аналогии с предыдущим, чтобы определить 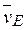 , надо сначала найти скорость т. D, принадлежащей одновременно стержням АВ и DE. Для этого, зная
, надо сначала найти скорость т. D, принадлежащей одновременно стержням АВ и DE. Для этого, зная 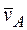 и
и 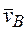 , строим мгновенный центр скоростей (МЦС) стержня AB; это т. С3, лежащая на пересечении перпендикуляров к
, строим мгновенный центр скоростей (МЦС) стержня AB; это т. С3, лежащая на пересечении перпендикуляров к 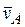 и
и 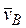 , восстановленных из т. А и В (
, восстановленных из т. А и В (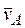 перпендикулярен стержню 1). По направлению вектора
перпендикулярен стержню 1). По направлению вектора 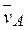 определяем направление вращения стержня АВ вокруг МЦС − С3. Вектор
определяем направление вращения стержня АВ вокруг МЦС − С3. Вектор 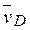 перпендикулярен отрезку С3D, соединяющему т. D и C3, и направлен в сторону вращения. Величину v D найдем из пропорции
перпендикулярен отрезку С3D, соединяющему т. D и C3, и направлен в сторону вращения. Величину v D найдем из пропорции
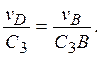 (3)
(3)
Чтобы вычислить С3D и C3B, заметим, что 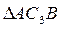 прямоугольный, т. к. острые углы в нем равны 30º и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда
прямоугольный, т. к. острые углы в нем равны 30º и 60º, и что C3B=АВsin30º=0,5AB=BD. Тогда  является равносторонним и C3B = С3D. В результате равенство (3) дает
является равносторонним и C3B = С3D. В результате равенство (3) дает
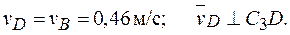 (4)
(4)
Так как т. Е принадлежит DE и одновременно стержню О2Е, вращающемуся вокруг О2, то  . Тогда, восстанавливая из точек Е и D перпендикуляры к скоростям
. Тогда, восстанавливая из точек Е и D перпендикуляры к скоростям 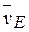 и
и 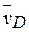 , построим МЦС − С2 стержня DE. По направлению вектора
, построим МЦС − С2 стержня DE. По направлению вектора 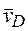 определяем направление вращения стержня DE вокруг центра С2. Вектор
определяем направление вращения стержня DE вокруг центра С2. Вектор 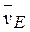 направлен в сторону вращения этого стержня. Из рис. К3б видно, что
направлен в сторону вращения этого стержня. Из рис. К3б видно, что  Составив теперь пропорцию, находим
Составив теперь пропорцию, находим 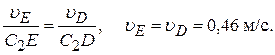 (5)
(5)
4. Определяем w2. Т. к. МЦС стержня 2 известен (т. С2), то
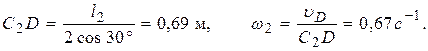 (6)
(6)
5. Определяем 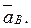 Т. В принадлежит стержню АВ. Чтобы найти
Т. В принадлежит стержню АВ. Чтобы найти 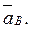 , надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию т. В. По данным задачи можем определить
, надо знать ускорение какой-нибудь другой точки стержня АВ и траекторию т. В. По данным задачи можем определить  где численно:
где численно:
 (7)
(7)
Вектор 
 направлен от т. А к т. О1,
направлен от т. А к т. О1, 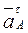 направлен перпендикулярно АО1, вектор
направлен перпендикулярно АО1, вектор 
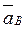 параллелен направляющим ползуна. Изображаем вектор
параллелен направляющим ползуна. Изображаем вектор 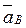 на чертеже, полагая, что он направлен в ту же сторону, что и
на чертеже, полагая, что он направлен в ту же сторону, что и 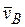 . Для определения
. Для определения 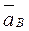 воспользуемся равенством
воспользуемся равенством 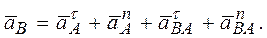 (8)
(8)
Изображая на чертеже векторы  (вдоль ВА от В к А) и
(вдоль ВА от В к А) и 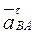 (в любую сторону перпендикулярно ВА); численно
(в любую сторону перпендикулярно ВА); численно 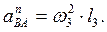 Найдя w3 с помощью построенного МЦС − С3 стержня 3, получим:
Найдя w3 с помощью построенного МЦС − С3 стержня 3, получим:
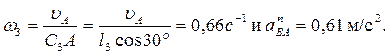 (9)
(9)
Таким образом, у величин, входящих в равенство (8), неизвестны только числовые значения a B и  . Их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси. Чтобы определить a B, спроектируем обе части равенства (8) на направление АВ (ось х), перпендикулярное неизвестному вектору
. Их можно найти, спроектировав обе части равенства (8) на какие-нибудь две оси. Чтобы определить a B, спроектируем обе части равенства (8) на направление АВ (ось х), перпендикулярное неизвестному вектору 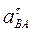 . Тогда получим
. Тогда получим 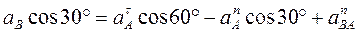 . (10)
. (10)
Подставив в равенство (10) числовые значения всех величин из (7) и (9), найдем, что
а В = 0,72 м/с2. (11)
Т. к. а В > 0, то, следовательно, вектор  направлен, как показано на рис. К3б.
направлен, как показано на рис. К3б.
6. Определяем e3. Чтобы найти e3, сначала определим 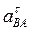 . Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
. Для этого обе части равенства (8) спроектируем на направление, перпендикулярное АВ (ось у). Тогда получим
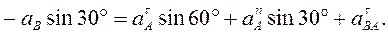 (12)
(12)
Подставив в равенство (12) числовые значения всех величин из (11) и (7), найдем, что 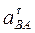 = -3,58 м/с2. Знак указывает, что направление
= -3,58 м/с2. Знак указывает, что направление 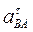 противоположно показанному на рис. К3б.
противоположно показанному на рис. К3б.
Теперь из равенства  = e3 l3 получим
= e3 l3 получим 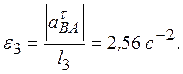
Ответ: uВ = 0,46 м/с; uЕ = 0,46 м/с; w2 = 0,67 с-1; аВ = 0,72 м/с2; e3 = 2,56 с-2.
Date: 2015-09-03; view: 1335; Нарушение авторских прав