Глобальные кинематические характеристики

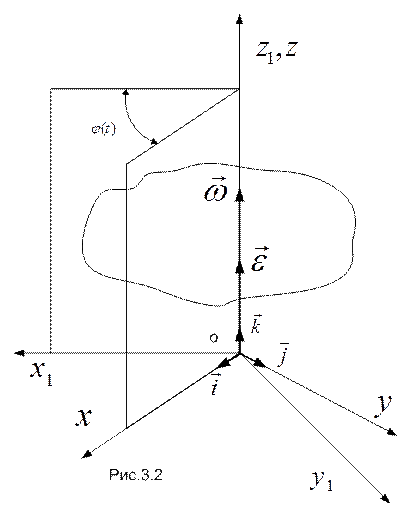
Тело, закрепленное в двух точках, обладает одной степенью свободы, выраженной в способности вращаться вокруг прямой, проходящей через точки закрепления и называемой неподвижной осью вращения. В некоторых случаях ось вращения может оказаться за пределами тела, например, при движении судна на циркуляции постоянного радиуса. Движение тела называется вращательным, если мысленно скрепленное с ним пространство имеет неподвижную ось вращения. В системах отсчета, связанных с опорами, указанное движение совершают, например, гребные винты, роторы турбин, маховики и пр.

Положение тела при вращении вокруг неподвижной оси определяется одной обобщенной глобальной координатой – двугранным углом 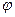между содержащими ось вращения плоскостями, одна из которых неподвижна (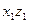), а другая жестко связана с телом (плоскость на рис.3.2).

Соответствующий двугранному линейный угол 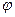называют углом поворота, а зависимость 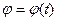- уравнением вращения твердого тела вокруг неподвижной оси. В правой координатной системе угол поворота считается положительным, если при взгляде навстречу оси наблюдается вращение твердого тела против хода часовой стрелки.

Пользуясь изменением 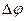угла поворота за время , вводят понятие угловой скорости тела в данный момент времени:

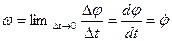. (3.3)

При 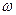>0 тело вращается в направлении возрастания угла поворота, а при 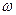<0 – в противоположном направлении. Для наших целей полезно ввести понятие вектора угловой скорости 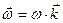, направленного вдоль оси вращения в ту сторону, откуда это вращение видно происходящим против хода часовой стрелки (рис.3.2). Единица измерения угловой скорости – радиан в секунду .

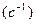Производная по времени от угловой скорости называется угловым ускорением:

. (3.4)

За единицу углового ускорения принимают радиан в секунду за секунду .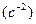

По аналогии с вектором угловой скорости вводят понятие вектора углового ускорения 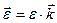, направленного вдоль оси вращения так, что при ускоренном вращении направление вектора 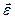совпадает с направлением вектора 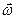(см. рис.3.2), а при замедленном вращении эти векторы направлены противоположно.

В частном случае равнопеременного (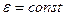) вращения аналитические зависимости между глобальными кинематическими характеристиками выглядят проще:

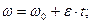
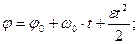
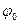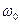где и - начальный угол поворота тела и начальная угловая скорость, соответственно.

Часто в технике равномерное вращение (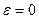) характеризуют частотой вращения - числом оборотов 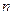, совершаемых телом за одну минуту вращения ().

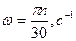Для определения скорости и ускорения точки (локальные кинематические характеристики) тела, вращающегося вокруг неподвижной оси, представим радиус-вектор точки М в подвижном базисе 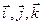(орты 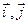поворачиваются вокруг неподвижного орта 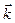) в виде

где 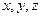- постоянные координаты выбранной точки тела в подвижном базисе.

По определению скорость точки М будет равна

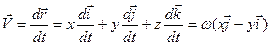. (3.5.а)

При дифференцировании было учтено, во-первых, постоянство координат точки и орта 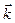в выбранном базисе и, во- вторых, формулы (1.12) для вычисления производных единичных ортов при их вращении вокруг неподвижной оси с угловой скоростью .

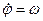Заметим, что полученное выражение может быть представлено как результат векторного произведения

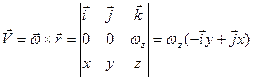. (3.5.б)

Оба выражения для скорости точки M дают один и тот же результат, так как при вращении вокруг неподвижной оси z .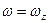

Окончательно для проекций вектора скорости точки М на оси подвижной координатной системы и его величины имеем:

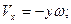
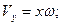
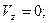
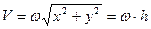. (3.6.а)

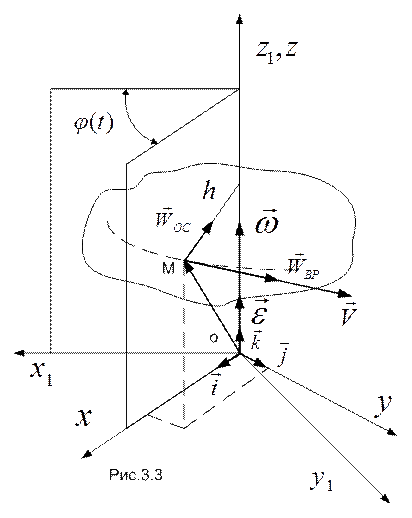
здесь 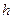- кратчайшее расстояние от точки М до оси вращения (см. рис.3.3).

Вычисление модуля векторного произведения дает этот же результат:

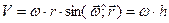. (3.6.б)

Для получения ускорения точки М продифференцируем по времени выражение (3.5.б):

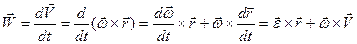. (3.7)

Первое слагаемое в (3.7) называют вращательным ускорением, а второе – осестремительным. Модули этих составляющих и модуль ускорения точки определяются выражениями

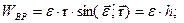
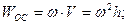
. (3.8)

На рис.3.3 изображены скорость и составляющие ускорения точки М при ускоренном вращении тела.

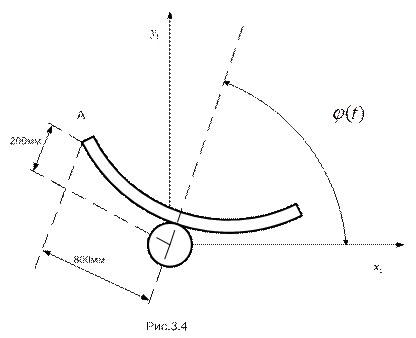
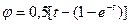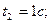
ПРИМЕР 3.1. Антенна радиолокатора, шарнирно укрепленная на мачте судна, начинает вращаться в горизонтальной плоскости (вид сверху изображен на рис.3.4). При этом угол между осью луча антенны и диаметральной плоскостью судна нарастает по закону . Найти угловую скорость и угловое ускорение антенны, а так же скорость и ускорение ее точки А для трех моментов времени: . Линейные размеры антенны указаны на рисунке.

РЕШЕНИЕ. Получим выражения для глобальных кинематических характеристик антенны:

;

;

.

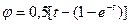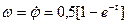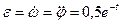Мгновенные значения этих величин для трех моментов времени сведем в таблицу 3.1.

В формулах (3.6) и (3.8) для определения скоростей и ускорений точки А, а так же ее осестремительных и вращательных составляющих, расстояние от точки А до оси вращения будет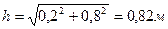

Результаты вычислений так же занесем в таблицу.

		0,18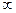
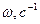
		0,32	0,50
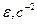
	0,50	0/18
		0,26
		0,08	0,20
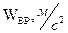
	0,41	0,15
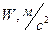
	0,41	0,17	0,20

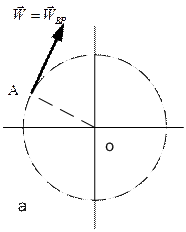
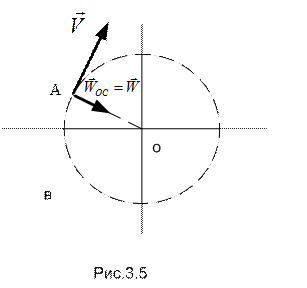
Из полученных данных следует, что антенна начинает разгоняться с довольно большим угловым ускорением, которое впоследствии уменьшается. Вскоре (хотя формально при 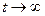) антенна выходит на режим установившегося вращения. Начальное ускорение точки А состоит только из вращательной составляющей (рис.3.5.а).

Скорость и ускорение точки А, а так же его составляющие, имеющие место на этапе разгона (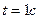), изображены на рис.3.5.б.

Скорость и ускорение на заключительном этапе движения изображены на рис.3.5.в.

Date: 2015-09-03; view: 634; Нарушение авторских прав