Б. Полярная и цилиндрическая координатные системы

В ситуациях, когда для любого момента времени известны расстояние 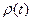от начала координат до рассматриваемой точки

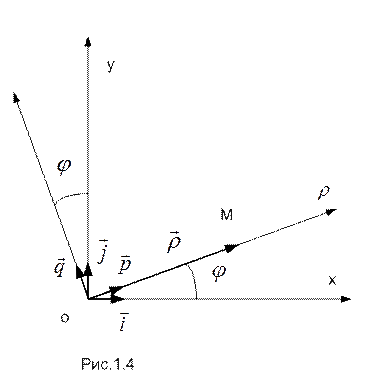
и направление на нее (например, движение торпеды по отношению к выпустившей ее неподвижной подводной лодке и т.п.), удобно воспользоваться полярной координатной системой (см. рис.1.4).

На рисунке 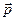и 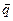- единичные орты осей полярной системы, а ее положение по отношению к плоской декартовой координатной системе определяется углом 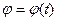поворота радиуса-вектора точки М. В этом случае

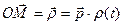. (1.11)

Очевидно, что в формулы для скорости и ускорения точки М будут входить производные от единичных ортов полярной системы, так как они, в общем случае, изменяют свое направление.

Запишем выражения, связывающие единичные орты полярной и декартовой координатных систем (см. рис.1.4):

.

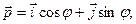
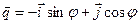Возьмем производные по времени от этих выражений:

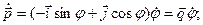
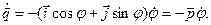(1.12)

Взяв первую производную от выражения (1.11) по времени, получим вектор скорости точки М как

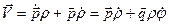(1.13)

здесь 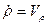- проекция скорости на радиус-вектор точки М, а 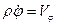- на ось, ему перпендикулярную.

Величину скорости рассчитываем по формуле

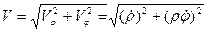. (1.14)

Взяв производную по времени от выражения (1.13), получим вектор ускорения точки М как

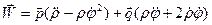(1.15)

здесь 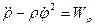- проекция ускорения на радиус-вектор точки М, а 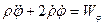- на ось, ему перпендикулярную. Величину ускорения рассчитываем по формуле

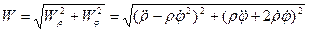. (1.16)

Цилиндрическая координатная система получается при наращивании полярной координатной системы ортогональной осью аппликат (см. рис.1.5).

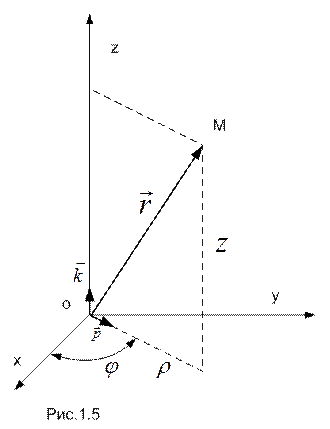
В таком случае выражение для радиуса-вектора точки М будет

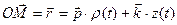(1.17)

Очевидно, что наличие ортогональной составляющей движения соответственно изменит выражения для скорости и ускорения:

;

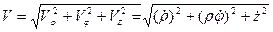; (1.18)

;

.

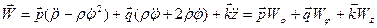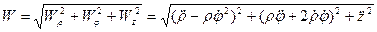ПРИМЕР 1.2. Судно двигается по прямой с постоянной скоростью 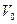. Гребной вал, ось которого параллельна поверхности воды, вращается с постоянной угловой скоростью 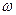. Диаметр гребного винта 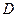. Найти траекторию, скорость и ускорение точки М – конца лопасти гребного винта (см. рис.1.6).

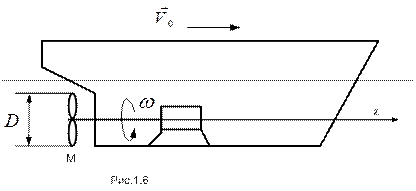
РЕШЕНИЕ. Расчет кинематических характеристик точки М выполним в цилиндрической координатной системе, ось z которой совпадает с осью гребного вала. Учитывая постоянство скорости судна и равномерность вращения вала, законы изменения координат записываются достаточно просто:

.

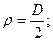
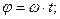
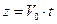Тогда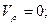

.

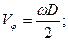
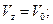
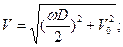
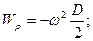
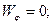
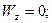
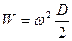Траектория точки М – винтовая линия, принадлежащая горизонтальному цилиндру диаметром 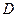, ось которого совпадает с осью гребного вала. Время одного оборота вала 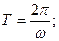шаг винтовой линии .

Замечание: рассмотренная задача могла быть решена и в декартовой координатной системе, но решение оказалось бы более трудоемким.

1.2.в. Криволинейная координатная система *

В общем случае в каждой точке пространства координат нужно записывать свою тройку базисных векторов 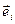. Совокупность независимых параметров 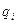объединяют одним понятием – криволинейные координаты, при этом векторы 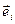являются их локальным базисом, в общем случае изменяющимся при переходе от одной точки пространства к другой. В рамках настоящего пособия ограничимся рассмотрением ортогональных криволинейных координат ( 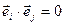при 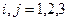). Именно такими были все координатные системы, рассмотренные нами ранее.

Уравнения движения в криволинейных координатах имеют вид

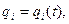
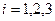(1.19)

Радиус-вектор любой точки пространства является непрерывной функцией координат :

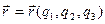(1.20) Например, в декартовой координатной системе его проекции запишутся так:

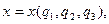
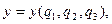
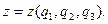(1.21)

Изменяя в (1.21) только одну из обобщенных координат, получают уравнение координатной линии 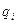(см. рис.1.7).

В каждой фиксированной точке 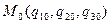пространства пересекаются три такие линии:

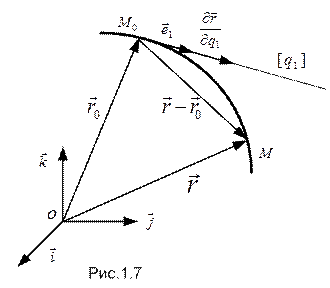
Линия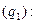

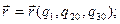
Линия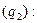

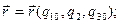
Линия

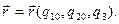
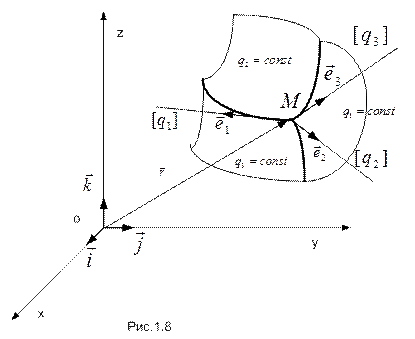
Касательные к координатным линиям, направленные в сторону возрастания координат, называют координатными осями 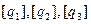в данной точке. Аналогично, изменяя сразу две координаты при фиксированной третьей, получают координатные поверхности (рис.1.8).

Орт координатной оси 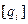находят путем деления вектора производной 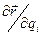(он направлен по касательной к координатной линии) на его модуль 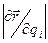. Для точек координатной линии (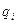) вектор в декартовой координатной системе имеет вид 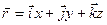, поэтому

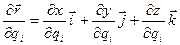, а для модуля вектора

(1.22)

Орт 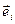равен

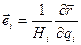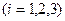, (1.23)

Коэффициенты 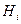являются функциями криволинейных координат и называются коэффициентами Ляме (дифференциальными параметрами Ляме). Для прямолинейных осей 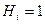. В ортогональных системах координат коэффициенты Ляме представляют собой множители при дифференциалах координат в выражениях дифференциалов дуг соответствующих координатных линий. Если элементарное перемещение равно

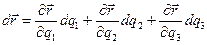, то квадрат дифференциала дуги равен

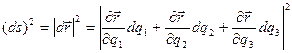, или, с учетом (1.23)

.

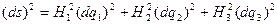Следовательно, дифференциалы дуг координатных линий (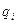) имеют вид

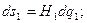
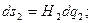
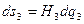. (1.24)

Часто коэффициенты Ляме находятся именно из этих соотношений. Формулы (1.23) позволяют находить косинусы углов между криволинейными координатными осями и осями декартовых координат:

.

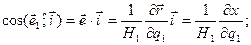
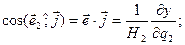
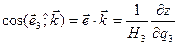Для нахождения проекций скорости точки М на оси криволинейных координат возьмем производную по времени от ее радиуса-вектора :

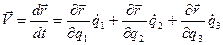(1.25)

где 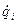- обобщенные скорости.

Согласно (1.23):

. (1.26)

Это выражение определяет разложение вектора скорости точки в локальном базисе криволинейных координатных осей:

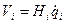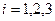, (1.27)

Модуль скорости находится как

,

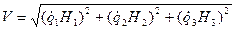а направление вектора скорости относительно координатных осей 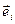задается направляющими косинусами

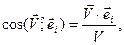
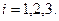
Для проекций ускорения удобно воспользоваться представлением

,

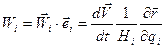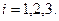
Откуда

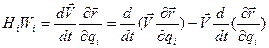. (1.28)

Из равенства (1.25) следует:

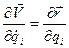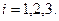, (1.29)

По определению полной производной

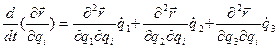
здесь

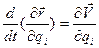. (1.30)

Подставляя в (1.28) значение 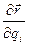из (1.29) и 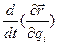из (1.30), получим

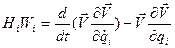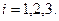, (1.31)

Учитывая, что 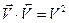, получим

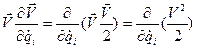и ,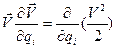

Запишем вектор ускорения точки М: .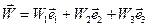

Тогда проекции ускорения на оси криволинейной системы координат будут

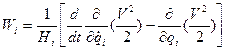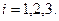, (1.32)

Модуль ускорения точки равен

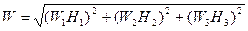, (1.33)

а направляющие косинусы соответственно

Зависимости (1.27) и (1.32) позволяют определять проекции скорости и ускорения в любой системе координат с ортогональным базисом (полярная, цилиндрическая, сферическая координатные системы и т. д.), целесообразный выбор которой зависит от вида конкретной задачи.

Пусть, например, движение точки задано в сферической (рис.1.9) координатной системе, т.е заданы функции . Требуется найти выражения для скорости и ускорения точки.

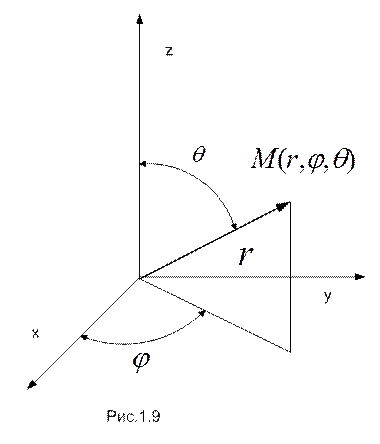
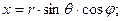
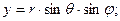
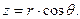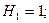
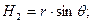
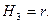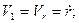
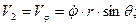
Связь декартовых координат со сферическими имеет вид Из формул (1.22) найдем коэффициенты Ляме Из формул (1.27) найдутся проекции скорости 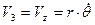и ее модуль как .

Затем по формулам (1.32) определяем проекции ускорения точки М на криволинейные координатные оси

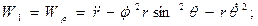
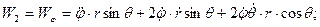
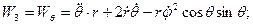
и модуль ускорения как квадратный корень из суммы квадратов его проекций.

Аналогичные зависимости для цилиндрической координатной системы читателю предлагается вывести самостоятельно и сравнить с формулами, полученными в пункте 1.2.б.

Date: 2015-09-03; view: 642; Нарушение авторских прав