Кинематика несвободной точки (движение по заданной траектории)

В технических приложениях выделяется круг задач о движении точки по заранее известной траектории (в общем – криволинейной). В таких случаях для описания движения точки

достаточно задаться лишь одной криволинейной координатой – длиной дуги 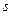, измеряемой вдоль траектории от избранного на траектории начала 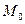(рис.2.1).

Движение точки определится законом изменения дуги как функции времени

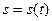. (2.1)

Дуговая координата 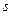точки, в общем случае, отличается от пройденного пути, который является неубывающей функцией времени (они совпадают при условии движения точки по траектории только в одну сторону).

Для определения скорости и ускорения несвободной точки напомним некоторые сведения из дифференциальной геометрии пространственных кривых. Плоскость 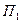, перпендикулярная касательной 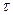к траектории в точке , называется нормальной плоскостью (рис.2.2). Любая прямая, лежащая в этой плоскости и проходящая через точку , направлена по нормали к кривой.

Касательную к траектории в точке 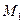, близко расположенной к точке , обозначим 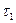, а дугу 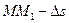(см. рис.2.1).

Если перенести прямую 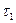параллельно самой себе в точку , то можно провести плоскость, содержащую прямые 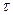и 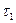; угол 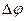между этими прямыми называется углом смежности. С уменьшением 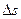до нуля эта плоскость, поворачиваясь вокруг прямой 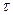, приближается к некоторому предельному положению – соприкасающейся плоскости 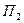(см. рис.2.2). Прямая, по которой пересекаются нормальная и соприкасающаяся плоскости, называется главной нормалью к кривой в точке . Нормаль, перпендикулярная главной нормали, называется бинормалью кривой. Плоскость 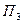, проходящая через касательную и бинормаль в точке М, называется спрямляющей плоскостью.

Нормальная, соприкасающаяся и спрямляющая плоскости образуют естественный трехгранник кривой в точке , а оси 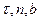являются его осями. Единичные орты этих осей образуют ортонормированный базис локальной естественной координатной системы.

Найдем проекции векторов скорости 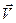и ускорения 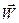точки в естественном базисе.

Радиус-вектор точки представляет собой сложную функцию времени 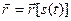, поэтому

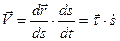. (2.2)

При выводе формулы учтено, что

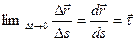- является единичным ортом касательной к траектории движения точки .

По определению ускорения имеем

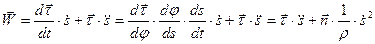. (2.3)

При выводе формулы учтено, что, во-первых,

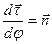- есть орт главной нормали, а, во-вторых, кривизна траектории , где 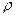- радиус кривизны траектории в точке .

Для доказательства первого обстоятельства продифференцируем по углу смежности скалярное произведение

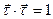. Получим, что 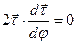, т.е. скалярное произведение двух векторов, расположенных в соприкасающейся плоскости, равно нулю. Это возможно только в случае их ортогональности.

Величина проекции ускорения на касательную

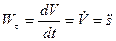называется касательным ускорением, оно характеризует изменение вектора скорости по величине. Величина проекции ускорения на главную нормаль

называется нормальным ускорением, оно характеризует изменение вектора скорости по направлению. Нормальное ускорение всегда направлено к центру кривизны траектории.

Полное ускорение точки равно

.

Заметим, что в выбранной координатной системе отсутствуют проекции скорости на главную нормаль и бинормаль, а так же проекция на бинормаль ускорения точки.

Рассмотрим несколько частных случаев движения точки.

1.Равномерное движение точки по прямой. Скорость движения не изменяется, поэтому равно нулю касательное ускорение.

Нормальное ускорение так же равно нулю (бесконечно большой радиус кривизны). Тогда

.

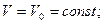
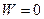2.Равнопеременное движение по прямой (). Нормальное ускорение равно нулю. Тогда

; .

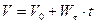3. Равномерное движение по окружности радиуса 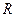. Вектор скорости направлен по касательной к окружности (к радиусу - под прямым углом). Скорость движения не изменяется по величине, поэтому равно нулю касательное ускорение. Полное ускорение равно нормальному, т.е. 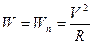. Ускорение направлено к центру окружности.

4. Равнопеременное движение по окружности радиуса 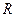. В этом случае скорость изменяется и по величине и по направлению, поэтому

; ; ; .

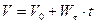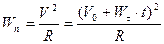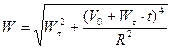ПРИМЕР 2.1. Центр тяжести катера, разгоняющегося из состояния покоя, описывает дугу окружности радиуса R=75м. Его касательное ускорение изменяется по закону 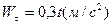. Определить скорость и ускорение центра тяжести катера в момент, когда он пройдет путь 50 м.

РЕШЕНИЕ. Интегрируя условие 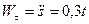дважды по времени с учетом нулевых начальных условий, получим:

; .

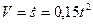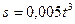Значение 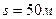достигается в момент времени 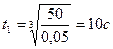. При этом скорость центра тяжести катера будет 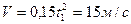, а касательное ускорение - . Тогда полное ускорение равно

.

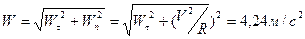Date: 2015-09-03; view: 877; Нарушение авторских прав