Розв’язування. Розглянемо рух механічної системи, що складається з вала , стержня та вантажу

Розглянемо рух механічної системи, що складається з вала 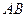, стержня 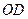та вантажу 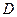. Для визначення невідомих реакцій застосуємо принцип Д’Аламбера. Проведемо осі 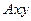, що обертаються разом з валом, таким чином, щоб стержень знаходився в площині 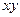, та зобразимо діючі на систему зовнішні сили: сили ваги 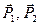, складові реакції підп’ятника і реакцію підшипника (рис.Д4.б).

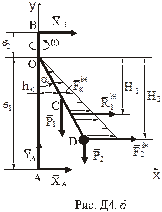За принципом Д’Аламбера прикладемо сили інерції елементів стержня та вантажу, вважаючи його матеріальною точкою. Враховуючи, що вал обертається рівномірно 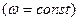, елементи стержня мають тільки нормальні прискорення 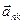, спрямовані до осі обертання, чисельно:

,

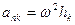де відстань елемента від осі.

Тоді сили інерції будуть спрямовані від осі обертання і чисельно:

,

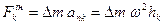де 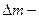маса елемента.

Оскільки всі пропорційні 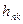, то епюра цих паралельних сил є трикутник і їх можна замінити рівнодійною , лінія дії якої проходить через центр ваги цього трикутника, тобто на відстані від вершини 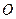, де 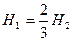(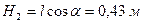, тобто ).

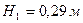Але, як звісно, рівнодійна будь якої системи дорівнює її головному вектору, а чисельно головний вектор сил інерції стержня:

,

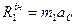де 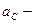прискорення центра мас стержня.

Як і будь-який елемент стержня, центр його мас має тільки нормальне прискорення:

Таким чином отримаємо:

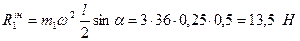
Аналогічно, сила інерції 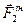вантажу спрямована від осі обертання, а чисельно:

.

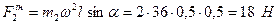Всі діючі на систему сили і сили інерції знаходяться в одній площині 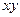, тому і реакції підп’ятника і підшипника 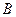також знаходяться в цій площині, що було враховано при їх зображенні.

За принципом Д’Аламбера, прикладені активні сили, сили реакції та сили інерції складають зрівноважену систему сил. Таким чином, для отриманої плоскої системи сил, складемо три рівняння умовної рівноваги:

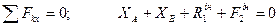(4.1)

(4.2)

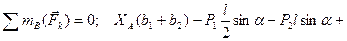
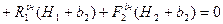(4.3)

Підставимо числові значення, та знайдемо невідомі реакції. Через те, що 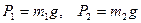, приймаючи , з рівняння (4.2) знайдемо :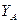

.

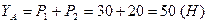З рівняння (4.3) знайдемо :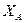

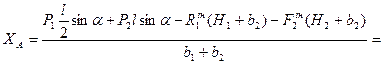
Підставимо отримане 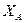в рівняння (4.1) і знайдемо :

.

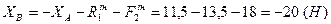Відповідь:

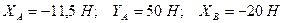. Знаки вказують на те, що сили 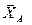та спрямовані протилежно показаним на рис. Д4.б

Date: 2015-09-03; view: 308; Нарушение авторских прав