
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розв'язування
|
|
Для дослідження руху кусень обрізі заміняємо матеріальною точкою масою 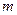 . Рух точки від початку лотка
. Рух точки від початку лотка  до місця падіння
до місця падіння  умовно розіб'ємо на дві ділянки: прямолінійну -
умовно розіб'ємо на дві ділянки: прямолінійну - 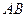 і криволінійну -
і криволінійну - 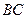 . Сили, що діють на точку на кожній з ділянок, постійні за величиною і напрямком.
. Сили, що діють на точку на кожній з ділянок, постійні за величиною і напрямком.

1. Розглянемо рух матеріальної точки на ділянці 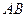 . Система координат з початком у точці
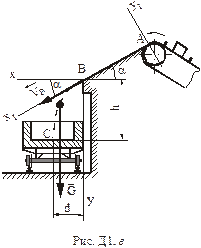
. Система координат з початком у точці  показана на рис.Д1.а. Зобразимо точку на ділянці
показана на рис.Д1.а. Зобразимо точку на ділянці 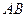 в довільний момент часу (рис.Д1.б). Зобразимо сили, що діють на точку в цей момент часу. Цими силами є: вертикальна за напрямком сила ваги
в довільний момент часу (рис.Д1.б). Зобразимо сили, що діють на точку в цей момент часу. Цими силами є: вертикальна за напрямком сила ваги 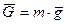 ; нормальна реакція похилої площини
; нормальна реакція похилої площини 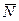 і сила тертя ковзання
і сила тертя ковзання 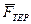 , спрямована уздовж площини лотка проти руху.
, спрямована уздовж площини лотка проти руху.
Запишемо динамічні рівняння руху точки в проекціях на обрані осі координат. Проекції сил, що співпадають з осями за напрямком, вважаємо додатними, а протилежні – від’ємними.
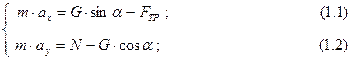
Якщо координата 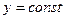 , маємо
, маємо 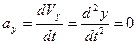 .
.
Тоді із (1.2) 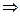
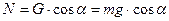 , що дозволяє обчислити силу тертя ковзання
, що дозволяє обчислити силу тертя ковзання  .
.
Тепер, якщо підставити значення 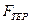 в (1.1), отримаємо:
в (1.1), отримаємо:
 ;
;
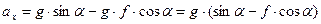
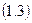
Перетворимо (1.3) в диференціальне рівняння шляхом заміни 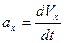 .
. 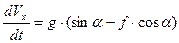
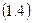
Інтегруючи (1.4) при 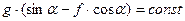 будемо мати:
будемо мати:
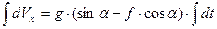
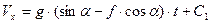
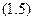
Константу 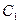 визначимо з початкової умови:
визначимо з початкової умови:  .
.
Тоді:
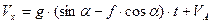
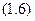
Для моменту часу  маємо
маємо  , тобто
, тобто
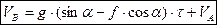

Аналогічно інтегруємо рівняння (1.6), враховуючи, що 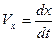 , а
, а 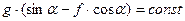 . Одержимо:
. Одержимо:


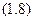
Константу 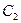 визначимо з початкової умови:
визначимо з початкової умови: 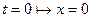 .
.
Тоді:
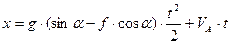
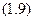
Для моменту часу  маємо
маємо  , тобто
, тобто
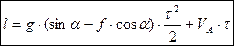

2. Розглянемо рух матеріальної точки на ділянці криволінійного руху 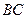 . Система координат з початком в точці
. Система координат з початком в точці 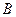 показана на рис. Д1.а. Зобразимо точку на ділянці
показана на рис. Д1.а. Зобразимо точку на ділянці 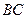 в довільний момент часу (рис. Д1.в). Зобразимо сили, що діють на точку в цей момент часу. На точку діє тільки одна сила - вертикальна сила ваги
в довільний момент часу (рис. Д1.в). Зобразимо сили, що діють на точку в цей момент часу. На точку діє тільки одна сила - вертикальна сила ваги 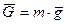 (опором повітря нехтуємо). Запишемо динамічні рівняння руху точки в проекціях на осі координат:
(опором повітря нехтуємо). Запишемо динамічні рівняння руху точки в проекціях на осі координат:
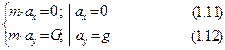
Перетворимо рівняння (1.11) у диференціальне і розв’яжемо його.
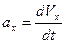

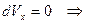
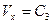
Використовуючи початкову умову  , знаходимо
, знаходимо 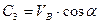 .
.
Тоді 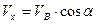
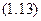
Перетворимо (1.13) у диференціальне рівняння і розв’яжемо його.
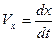

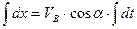
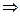
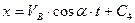 .
.
З початкової умови: 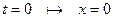 маємо
маємо 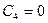 , а
, а

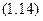
Підставляючи в (1.14) 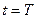 , знайдемо координату
, знайдемо координату 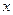 точки падіння
точки падіння  :
:
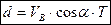

Перетворимо рівняння (1.12) у диференціальне і розв’яжемо його.
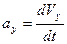
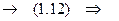
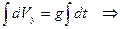
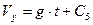
З початкової умови:  маємо
маємо 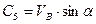
Тоді 
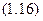
Перетворимо рівняння (1.16) у диференціальне і розв’яжемо його:
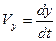

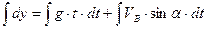
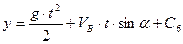
З початкової умови маємо:  . Тому
. Тому  , а
, а
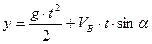
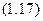
Підставляючи в (1.17) 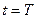 , знайдемо координату
, знайдемо координату 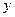 точки падіння
точки падіння 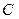 :
:

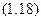
Розглянемо систему рівнянь (1.7), (1.10), (1.15) і (1.18). Чотири рівняння містять чотири невідомих параметри: 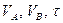 і
і 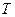 , тобто система має розв’язок. Після підстановки відомих величин маємо наступне:
, тобто система має розв’язок. Після підстановки відомих величин маємо наступне:
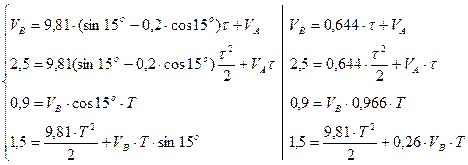
Виконавши обчислення, отримаємо:
 ;
; 
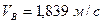 ;
; 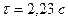 ;
;  .
.
Частину із знайдених величин потрібно визначити за умовою задачі.
Аналіз рівняння (1.15) дозволяє відповісти ще на одне з питань умови - дальність польоту точки не залежить від її маси.
Відповідь.
1. Необхідна швидкість стрічки транспортера 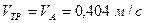 .
.
2. Дальність польоту шматків обрізі не залежить від їх маси.
3. Швидкість кусня в момент відриву від лотка 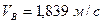 .
.
Date: 2015-09-03; view: 368; Нарушение авторских прав