Топологические пространства и топологии

Комментарий. Функция 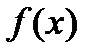называется непрерывной в точке 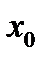(по Коши), если для любого 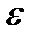> 0 существует 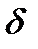= 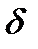(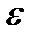) > 0, такое, что как тольк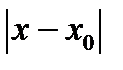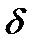о < , то 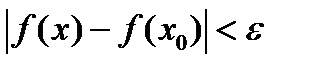.Удобная модификация: Под окрестностью точки понимается любое открытое множество, содержащее эту точку. Тогдафункция 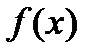называется непрерывной в точке 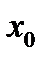, если для любой окрестности U точки существует окрестность V точки 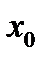, такая, что из того, что 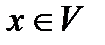следует, что .

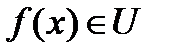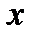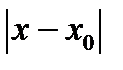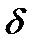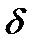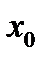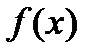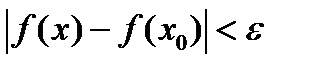Для числовых функций эти определения эквивалентны, поскольку, с одной стороны, множество точек , таких, что < , является -окрестностью точки , а множество точек , что , является 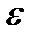-окрестностью точки , а с другой стороны, внутри любой окрестности U точки содержится 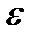-окрестность для достаточно малого 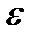(соответственно в любой окрестности V точки 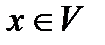содержится 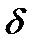- окрестность для достаточно малого ).

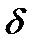Можно ли дать определение непрерывности для отображения, которое определяется уже не для чисел, а для произвольных носителей, то есть для элементов произвольных множеств? Нет, потому, что неясно, что понимать под окрестностью точки на произвольных носителях.Надо предварительно ввести понятие окрестности точки на произвольном множестве, а потом понятие 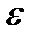-окрестности, как частного случая окрестности вообще.

Множество, на котором корректно введено понятие 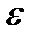- окрестности точки на произвольных множествах, называется метрическим пространством. Множество, на котором "правильно" введено понятие окрестности точки на произвольных множествах, называется топологическим пространством. Понятие топологического пространства является минимальным для того, чтобы корректно определить понятие непрерывного отображения. Оно обобщает понятие геометрической фигуры в том смысле, что здесь отвлекаются от размера или точного положения частей фигуры в пространстве, и сосредотачиваются только на взаимном расположении частей. Метрическое пространство является частным случаем топологического. Таким образом, любая метрика порождает топологию и даже не одну. Однако, обратное, вообще говоря, не верно: существуют топологии, не порождаемые никакой метрикой.

Для корректного определения понятия окрестности точки в произвольном множестве вспомним, что множество называется открытым, если для любой его точки достаточно малый шар с центром в этой точке (то есть 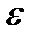-окрестность для достаточно малого 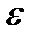) целиком входит в это множество.

Ранее было показано, что в метрических пространствах для открытых множеств выполняются два свойства: объединение любого (даже бесконечного) набора открытых множеств есть открытое множество и пересечение конечного числа открытых множеств есть открытое множество. Приняв их за аксиомы, получим топологию в аксиоматике Александрова. В силу принципа двойственности топологию можно также задать, описав множество всех замкнутых множеств (т.е. всех дополнений к открытым множествам).

Определение 1. Рассмотрим произвольное множество X – носитель топологического пространства. Множество 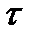его подмножеств называется топологией на X, если выполнены следующие свойства:

- Все X и пустое множество 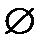принадлежат ,

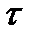- Объединение конечного или бесконечного семейства множеств 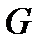, принадлежащих 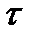, то есть 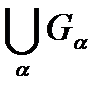тоже принадлежит ,

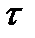- Пересечение конечного числа множеств 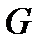, принадлежащих 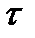, то есть 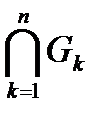принадлежит .

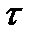Определение 2. Носитель топологического пространства – множество X вместе с заданной на нем топологией 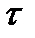называется топологическим пространством Т=(Х, ).

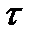Комментарий. Поопределению,все подмножества X, принадлежащие 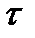, считаются (называются) открытыми множествами. Множества 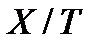, дополнительные к открытым, называются замкнутыми множествами топологического пространства 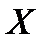. Всё множество X и пустое множество 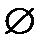считаются открытыми и замкнутыми одновременно.

Date: 2015-09-03; view: 423; Нарушение авторских прав