Сравнение метрик (норм)

Определение 1. Метрика (норма) ρ₁ сильнее, чем метрика (норма) ρ₂, если из сходимости последовательности 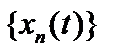по ρ₁ следует её сходимость по ρ₂, но существует 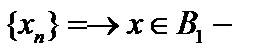хоть одна последовательность, которая сходится по норме ρ₂, но не сходится по норме ρ₁.

Определение 2. Две метрики (нормы) ρ₁ и ρ₂ эквивалентны, если из сходимости последовательности 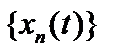по ρ₁ следует её сходимость по ρ₂ и наоборот.

Определение 2^*. Две метрики (нормы) ρ₁ и ρ₂ эквивалентны, если существуют или .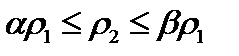

Теорема 1. В любых конечномерных пространствах все метрики (нормы) эквивалентны.

Рассмотрим нормированное пространство 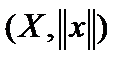, , 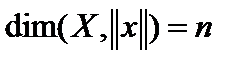система векторов 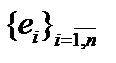образует базис в нём, то есть

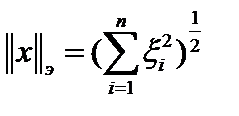. Эвклидова норма , а 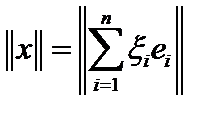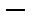ещё одна норма в этом пространстве. Оценим её. 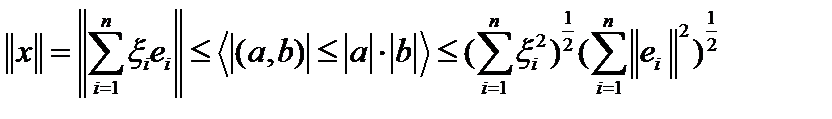. Обозначив 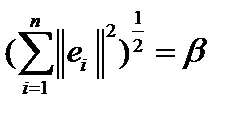, получим 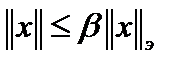. Покажем, что 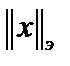в свою очередь подчинена 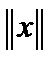. Рассмотрим функцию 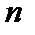переменных 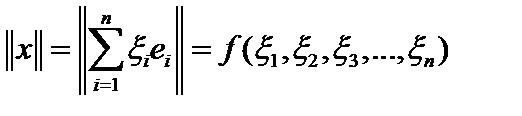на сфере . Она непрерывна, так как 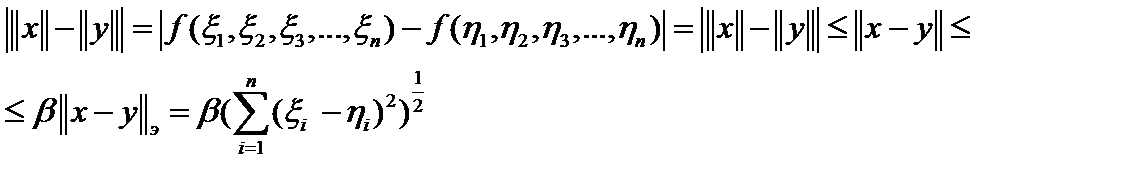и стремится к нулю при 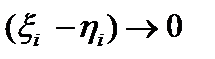. Единичная сфера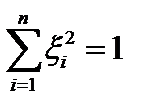 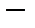замкнутое ограниченное множество, поэтому на ней, в соответствии с теоремой Вейерштрасса, функция достигает своих точных верхней и нижней граней. То есть на сфере 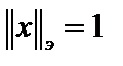имеем .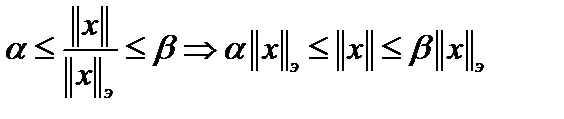

Пример. Доказать, что метрика 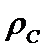пространства 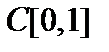сильнее метрики 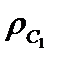пространства .

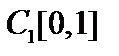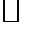
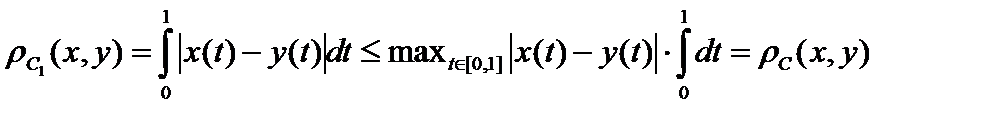, то есть 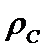не слабее 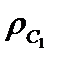. Теперь укажем последовательность 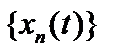, которая сходится по 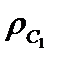, но не сходится по 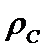. Эта последовательность стандартный пробник функционального анализ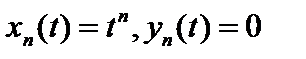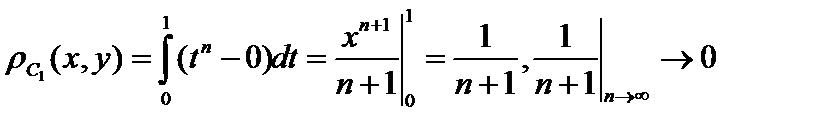а, . , а 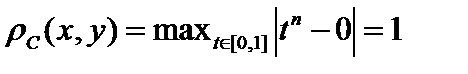, то есть эта последовательность сходится по 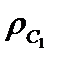, но не сходится по .

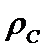Комментарий. В линейной алгебре показывалось, что все линейные структуры изоморфны, то есть существует возможность установить биекцию между ними. Эта теорема утверждает большее отображение между метрическими пространствами не только взаимно однозначно, но и взаимно непрерывно, то есть гомеоморфно. В конечномерных пространствах все метрики (нормы)топологически эквивалентныв следующем смысле: для шара 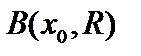радиуса R с центром в точке 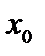, построенного на основе одной из норм, можно построить вписанный в него и описанный вокруг него шары, построенные на основе другой нормы (разумеется, другого радиуса). В бесконечномерных пространствах это не так.

Пример. Покажем, что чебышевская норма, по крайней мере, не слабее гёльдеровской, а дифференциальная не слабее чебышёвской. 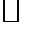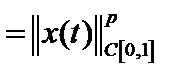, но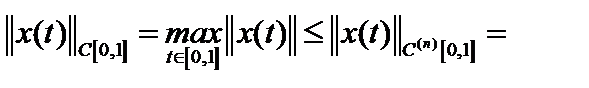

.

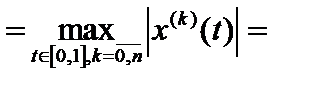
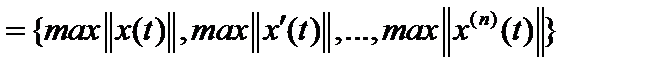Date: 2015-09-03; view: 838; Нарушение авторских прав