Практическое занятие №2 по теме

«Общие теоремы динамики механической системы»

Пример решения задачи №1

Условие.

Вагонетка, вес которой вместе с полезной нагрузкой 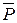составляет 850 Н, при движении по горизонтальному пути испытывает сопротивление, величина которого составляет 0,01 P. Рабочий толкает вагонетку с силой 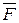, равной 17 Н. Через какое время рабочий сообщит вагонетке скорость 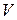, равную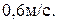

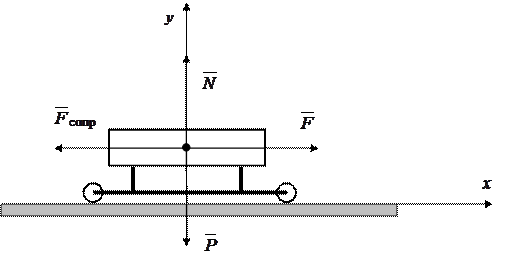Рис. 30. Движение вагона под действием силы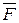

Решение.

1. Покажем силы, действующие на вагонетку.

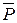- сила тяжести, 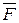- сила, с которой рабочий толкает вагонетку, 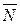- нормальная реакция опоры, 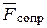- сила сопротивления движению.

2. Решение данной задачи сводится к рассмотрению движения материальной точки (центра тяжести вагонетки) на которую действует равнодействующая сила, определяемая по формуле

.

3. Введем систему координат и спроектируем уравнение пункта два на ось х, получим

.

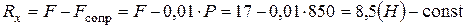4. Применим теорему об изменении количества движения в интегральной форме:

,

Проинтегрировав правую часть, получим

.

Учитывая, что при 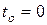, получим

.

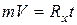Выражая время из последней формулы, получим

.

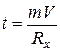Учитывая, что , и подставляя численные значения, получим

.

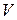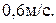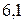Ответ: рабочий сообщит вагонетке скорость , равную через с.

Список рекомендуемой литературы

1. Будник, Ф.Г. Сборник задач по теоретической механике: учеб. пособие для вузов / Ф.Г. Будник. М., «Высшая школа», 1987.

2. Колесников, К.С. Сборник задач по теоретической механике / К.С. Колесников. М., «Наука», 1989.

Пример решения задачи №2

Условие.

Для заданной механической системы, состоящей из двух грузов массой М ₁ и М ₂ и составного блока массой М ₃, определить ускорения грузов, угловое ускорение блока, а также реакции опор блока, если известны радиус большой ступени блока R, радиус малой ступени r и радиус инерции r _ин.

Рис. 31. Механическая система из двух грузов и неподвижного блока

Решение.

Механическая система состоит из пяти тел: груза 1, груза 2, составного блока 3 и двух абсолютно невесомых нерастяжимых нитей.

1. Покажем внешние силы, действующие на систему.

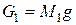- сила тяжести, действующая на груз 1,

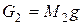- сила тяжести, действующая на груз 2,

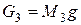- сила тяжести, действующая на составной блок 3,

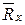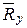, - реакции опоры блока.

2. Предположим, что под действием внешних сил груз 1 опускается, груз 2 поднимается, а блок 3 вращается против часовой стрелки.

3. Покажем скорости тел системы.

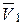- скорость груза 1, совершающего поступательное движение,

- скорость груза 2, совершающего поступательное движение,

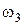- угловая скорость блока 3, вращающегося вокруг точки О.

4. Выразим кинематическую зависимость между скоростями тел системы, учитывая, что нить нерастяжима:

, .

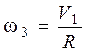5. Определим кинетические моменты тел системы относительно точки О.

5.1. Определим кинетический момент груза 1, по формуле

.

5.2. Определим кинетический момент груза 2, по формуле

.

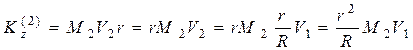5.3. Определим кинетический момент блока 3, по формуле

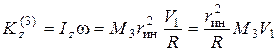, где .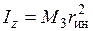

Кинетические моменты нитей 4 и 5 равны нулю, так как нити

приняты невесомыми.

6. Определяем кинетический момент системы.

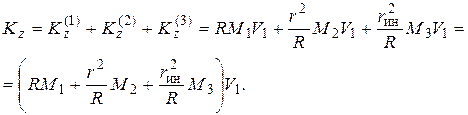
7. Определим сумму моментов внешних сил:

.

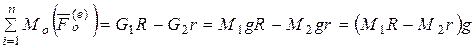8. Применим теорему об изменении кинетического момента:

.

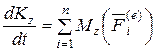Подставляя значения кинетического момента 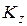из пункта 6 и суммы моментов 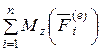из пункта 7, получим

.

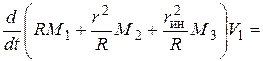
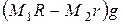Продифференцировав, получим

,

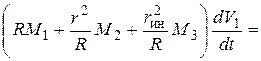
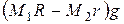учитывая, что 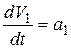- ускорение груза 1, получим

.

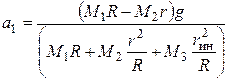9. Определим ускорение груза 2 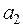и угловое ускорение блока 3 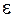, учитывая, что нити нерастяжимы.

,

.

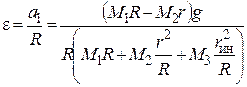10. Определим реакции опоры блока.

10.1. Применим теорему об изменении количества движения.

, ,

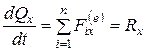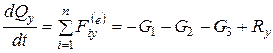10.2. Определим проекции количества движения системы:

, .

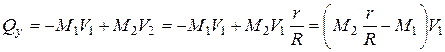Подставляя в уравнения пункта 10.1, получим ,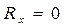

,

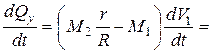
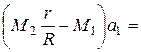
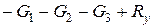где - ускорение груза 1.

Выражая реакцию 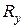, получим

,

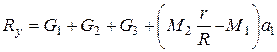подставляя силы тяжести из пункта 1, окончательно получим

.

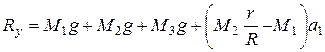Ускорение 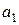определяется в пункте 8.

Ответ: ускорение груза 1, груза 2 и угловое ускорение блока 3 определяются по формулам

, ,

.

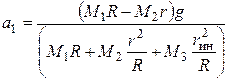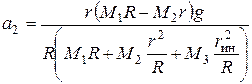Реакции опоры блока определяются формулами , .

Список рекомендуемой литературы

1. Колесников, К.С. Сборник задач по теоретической механике / К.С. Колесников. М., «Наука», 1989.

2. Бражниченко, Н.А. Сборник задач по теоретической механике: учеб. пособие для вузов / Н.А. Бражниченко. М., «Высшая школа», 1974.

Пример решения задачи №3

Условие.

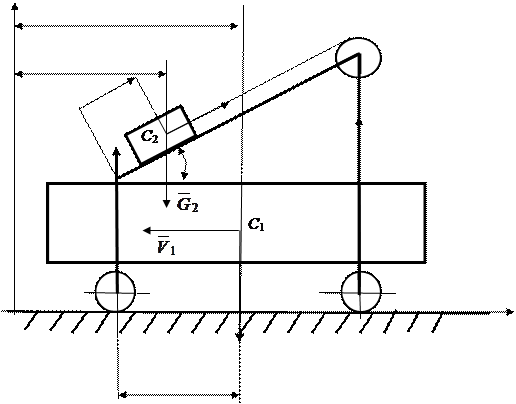
На горизонтальной платформе массой М ₁ установлена наклонная плоскость АВ, образующая с горизонтом угол α. По этой плоскости с помощью лебедки поднимается груз массой М ₂ таким образом, что расстояние АС ₂ изменяется по закону 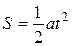. В начальный момент времени вся система находится в покое. Определить скорость, с которой будет двигаться платформа, сопротивлением платформы пренебречь.

Решение.

Рассматривается механическая система, состоящая из двух тел: платформы 1 и груза 2.

Рассмотрим решение задачи двумя способами.

Первый способ основан на применении теоремы об изменении количества движения системы.

1. Введем систему координат.

2. Покажем внешние силы, действующие на систему.

G ₁ = М ₁ g – сила тяжести, действующая на платформу,

G ₂ = М ₂ g - сила тяжести, действующая на груз,

3. Применим теорему об изменении количества движения. Так как все внешние силы вертикальны на основании (4.11^/), получим

.

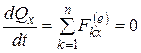По условию задачи система в начальный момент времени неподвижна, следовательно, .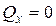

4. Определим проекцию вектора количества движения на ось Ox.

Количество движения системы определим как сумму количеств движения платформы и тележки:

,

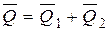где 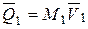- вектор количества движения платформы 1,

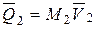- вектор количества движения груза 2.

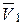- скорость центра масс платформы 1,

- скорость центра масс груза 2.

Проецируя на ось Ox, получим

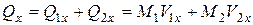
y

x_{C 1}

B

x_{C 2}

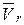
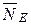
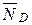
D E

x

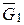
L

Рис. 32. Механическая система из подвижной платформы и груза

Учитывая, что 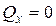, получим

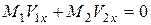. (А)

Скорость центра масс платформы 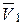направлена по оси Ox, так как платформа совершает поступательное движение вдоль этой оси.

Определим проекцию скорости центра масс груза на ось Ox, учитывая, что груз совершает сложное движение. За переносное движение примем поступательное движение платформы. За относительное движение примем движение груза по наклонной плоскости по закону Ошибка! Ошибка связи.. Таким образом, скорость платформы является скоростью переносного движения груза, то есть. 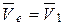. Относительную скорость определим по формуле

_.

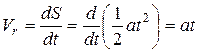По теореме сложения скоростей при сложном движении, получим

_.

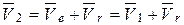Проецируя последнее выражение на ось Ox, получим

,

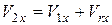Предположим, что платформа движется в право, тогда .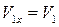

Учитывая, что груз поднимается по наклонной плоскости (рис. 33), получим

.

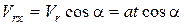Окончательно для получим

_.

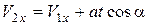Подставляя полученную формулу в выражение (А), получим

_.

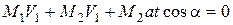Выражая 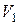, окончательно получим

_.

Знак минус в полученном выражении указывает, что направление скорости платформы было выбрано неверно. Платформа будет перемещаться влево.

Рассмотрим решение задачи вторым способом, который основан на применении теоремы о движении центра масс системы.

1. Определим координаты центра масс системы.

Обозначим C ₁ центр тяжести платформы, C ₂ центр тяжести груза.

Используя выражение для статического момента массы относительно оси, получим

.

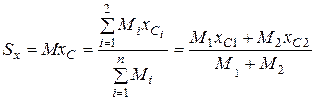2. Применим теорему о движении центра масс (4.16^/), получим

.

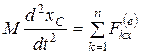Учитывая, что все силы, действующие на систему вертикальны, получим

,

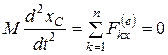следовательно, .

Так как в начальный момент времени система по условию задачи неподвижна: 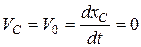, получим

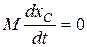
и, следовательно,

.

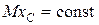Используя выражение пункта 1, получим

.

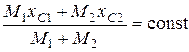Следовательно,

.

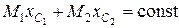Определяя из геометрических соображений выражение для координаты центрам масс груза 2, и подставляя в полученное выражение, получим

,

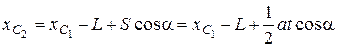следовательно,

.

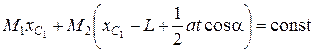Дифференцируя последнее выражение по времени, получим

.

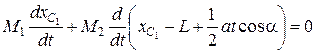Определяя производные, раскрывая скобки и выражая 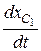, окончательно получим

.

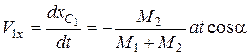Ответ: платформа перемещается влево со скоростью .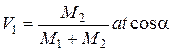

Список рекомендуемой литературы

1. Будник, Ф.Г. Сборник задач по теоретической механике: учеб. пособие для вузов / Ф.Г. Будник. М., «Высшая школа», 1987.

2. Колесников, К.С. Сборник задач по теоретической механике / К.С. Колесников. М., «Наука», 1989.

ЗАДАНИЕ И ВАРИАНТЫ ИСХОДНЫХ ДАННЫХ ДЛЯ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ. УКАЗАНИЯ ПО ИХ ВЫПОЛНЕНИЮ

Date: 2015-09-03; view: 1065; Нарушение авторских прав