Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Момента системы
|
|
Напишем теорему об изменении момента количества движения относительно центра О для k -й точки:
. 
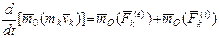, то есть производная по времени от кинетического моментасистемы относительно центра O равна главному моменту внешних сил, действующих на систему, относительно этого центра.
По аналогии для проекций, если
, 
, 
, 
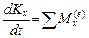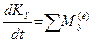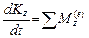, то есть производная по времени от кинетического момента системы 
(
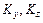) относительно неподвижной оси 
(
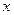) равна главному моменту всех внешних сил, действующих на систему, относительно этой оси.
Следствие. Закон сохранения кинетического момента системы.
Если 
,то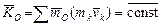 
, то есть если главный момент внешних сил, действующих на систему, относительно центра в течение некоторого времени равен нулю, то ее кинетический момент относительно центра в течение этого времени остается постоянным. Это же справедливо и для проекций на оси: если 
, 
, 
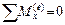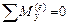, то 
, 
, 
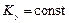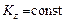.Внутренние силы системы не могут изменить ее кинетический момент.Примером служит скамья Жуковского. Если человек, сидящий на ней, раздвигает гантели (увеличивается момент инерции системы относительно оси вращения), то скорость вращения скамьи уменьшается, а при их сближении она увеличивается (момент инерции уменьшается), что соответствует соотношению
.
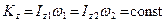Вопрос 35 Диф уравнения ПОСТУПАТЕЛЬНОЕ,вращательного,плоского ДВИЖЕНИЕ
В поступательном движении твердого тела все его точки движутся так же, как и его центр масс. Поэтому дифференциальные уравнения его движения являются дифференциальными уравнениями движения тела:
,
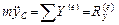, (10.1)
,
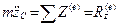где m – масса тела; ∑X (е), ∑Y (е), ∑Z (е) – алгебраические суммы проекций внешних сил на координатные оси; Rx(е), Ry(е), Rz(е) – проекции главного вектора внешних сил на эти оси.
Date: 2015-09-03; view: 387; Нарушение авторских прав