Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Плоское движение
|
|
Пусть твердое тело совершает плоское движение так, что центр масс С движется в плоскости чертежа (рис. 10.2). В динамике за полюс принимается центр масс тела, а не произвольная точка (как в кинематике).
Уравнения движения плоской фигуры
,
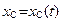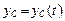, (10.4)
.
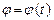При известных силах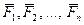 
дифференциальные уравнения плоского движения твердого тела выглядят так:
,
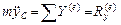, (10.5)
,
где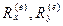 
– проекции главного вектора внешних сил на координатные оси, 
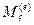– главный момент внешних сил относительно оси 
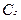, перпендикулярной к плоскости чертежа.
Если траектория центра масс задана, то удобно использовать дифференциальные уравнения движения точки С в проекциях на естественные координатные оси
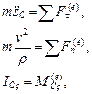(10.6)
где sc – путь центра масс, vc – его скорость,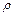 
– радиус кривизны его траектории.
Вопрос 36 ФИЗИЧЕСКИЙ МАЯТНИК ТЕОРЕМА ГЮЙГЕНСА
Физический маятник – это твердое тело, имеющее горизонтальную ось вращения, не проходящую через его центр тяжести и находящееся под действием только силы тяжести (рис. 10.3). Ось вращения физического маятника называется осью привеса маятника.
дифференциальное уравнение вращательного движения маятника имеет вид (реакции Z0, Y0 момента не дают, а моментом силы трения в шарнире О пренебрегаем)
,
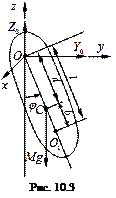
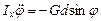где Iх – момент инерции маятника относительно оси привеса, G = Мg – вес маятника, d – расстояние от центра тяжести маятника до оси привеса.
Перепишем уравнение иначе
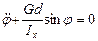. Это дифференциальное уравнение качаний физического маятника.
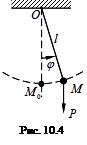Для математического маятника (рис. 10.4) уравнение имеет вид
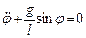. (10.8)
,
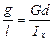откуда
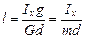. (10.9)
Таким образом, приведенная длина физического маятника есть длина такого математического маятника, период качаний которого равен периоду качаний данного физического маятника.
По формуле Штейнера-Гюйгенса имеем
,
где iCx – радиус инерции маятника относительно оси Cx. 
. (10.10)
Таким образом, если ось качаний физического маятника сделать осью привеса, то прежняя ось привеса станет его осью качаний (суть теоремы Гюйгенса о взаимности оси привеса и оси качаний физического маятника).
При малых углах 
(до 150)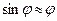 
, тогда формула (10.7) примет вид
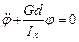, или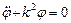 
, (10.11)
где 
– частота колебаний маятника.
Общее решение этого уравнения:
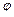= C 1cos kt + C 2sin kt, или 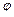= a sin (kt+β), (10.12)
где а – амплитуда колебаний в радианах, β – начальная фаза колебаний. Они, как и произвольные постоянные интегрирования C 1, C 2, определяются из начальных условий.
Период малых колебаний физического маятника
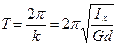. (10.13) С учетом выражения (10.9)
.
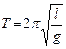Вопрос 37 СИЛЫ ИНЕРЦИИ. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ
.
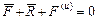Формула описывает состояние динамического равновесия МТ и выражает принцип Даламбера: при движении МТ непосредственно приложенная к ней сила, реакция связей и сила инерции точки составляют систему сил, эквивалентную нулю, то есть находящуюся в динамическом равновесии.
МТ движется с ускорением 
, так как на нее действуют тела с силой (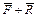
). 
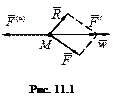
Силы инерции условно прикладывают к МТ и рассуждают о ее динамическом равновесии. Этот прием носит название «метод кинетостатики Так как полное ускорение МТ можно разложить на касательную и нормаль (рис. 11.2)
,
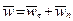то силу инерции можно представить в виде геометрической суммы векторов
,где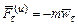 
– касательная сила инерции, направленная по касательной к траектории точки; 
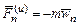– нормальная (центробежная) сила инерции, направленная по нормали к траектории в сторону ее выпуклости.
Date: 2015-09-03; view: 476; Нарушение авторских прав