Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Частные случаи
Поступательное движение .
,
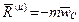то есть при поступательном движении силы инерции твердого тела приводятся к равнодействующей 
, проходящей через центр масс.
Вращательное движение. Положим, тело вращается вокруг оси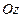 
, перпендикулярной к плоскости чертежа (рис. 11.3), с которой совпадает плоскость материальной симметрии тела. Приводя силы инерции к центру О, получим результирующую силу и пару, лежащие в плоскости симметрии. Тогда с учетом равенства (11.11) имеем
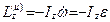, (11.12)
то есть система сил инерции вращающего тела приводится к силе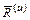 
, проходящей через центр О, и паре с моментом 
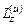, лежащей в плоскости симметрии тела.
Вращение вокруг неподвижной оси, проходящей через центр масс тела. В этом случае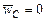 
, следовательно, 
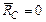. Поэтому система сил инерции приводится к паре сил с моментом 
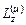, лежащей в плоскости симметрии тела.
Плоскопараллельное движение. Положим, тело имеет плоскость симметрии и движется параллельно ей.В этом случае система сил инерции приводится к лежащим в плоскости симметрии силе инерции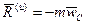 
, приложенной в центре масс, и паре сил с моментом 
.
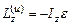. Вопрос 39 ТИПЫ СВЯЗЕЙ. ПОНЯТИЕ ИДЕАЛЬНЫХ СВЯЗЕЙ
Существуют два основных типа связей: голономные и неголономные.
Голономными называются такие связи, которые выражаются или уравнениями относительно координат, или неравенствами, или же интегрируемыми дифференциальными уравнениями относительно координат. Голономные связи ещё называют геометрическими.
Неголономными называются связи, выраженные неинтегрируемыми дифференциальными уравнениями относительно координат, то есть уравнениями, содержащими не только координаты точек, но и их производные по времени.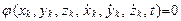 
.
Связи, не зависящие от времени, называются склерономными (то есть не изменяемые по своему виду, подобно неизменяемому твердому телу), или стационарными.
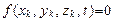. (12.2)
Связи, зависящие от времени, называют реономными (подвижными), или нестационарными.
Двусторонними голономными связями называются связи, выражающиеся уравнениями, например, для одной точки
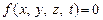. (12.3)
Односторонними (освобождающими, неудерживающими) называются связи, выраженные неравенствами. Например, неравенство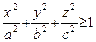 
означает, что точка может находиться на поверхности эллипсоида или сойти с него во внешнюю область.
ИДЕАЛЬНЫЕ СВЯЗИ Идеальными связями, или связями без трения, называются такие связи, при которых сумма элементарных работ их реакций равна нулю на любом возможном перемещении системы. К их числу относятся все стационарные голономные связи без трения.Для k -й точки введем обозначения сил: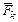 
– равнодействующая активных сил, 
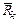– равнодействующая реакций связей, 
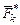– равнодействующая всех сил.
Тогда
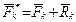. (12.4)
Вопрос 40 ПРИНЦИП ВОЗМОЖНЫХ (ВИРТУАЛЬНЫХ) ПЕРЕМЕЩЕНИЙ
Пусть имеется система несвободных МТ, находящаяся в равновесии.
Выделим материальную точку Мк. Обозначим: 
– равнодействующая активных сил, 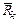– равнодействующая реакций связей.
|
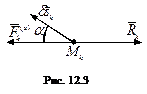Так как система находится в равно-весии, то 
(рис. 12.3).
Сообщим системе возможное перемещение, тогда точка Мк получит элементарное перемещение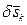 
. Сумма элементарных работ на возможном перемещении
.
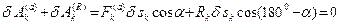Написав такие равенства для всех точек и просуммировав их почленно, получим
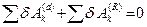. (12.6)
Для идеальных связей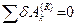 
, следовательно,
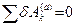. (12.7)
Нетрудно доказать и обратное: если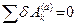 
, то система находится в равновесии. Это выражает принцип возможных (виртуальных) перемещений: для равновесия системы с идеальными связями необходимо и достаточно, чтобы равнялась нулю сумма элементарных работ всех приложенных к ней активных (внешних) сил на любом возможном перемещении системы из положения равновесия.
Выражая работу сил через проекции, имеем
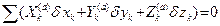, (12.8)
где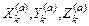 
– проекции приложенных к системе активных сил, 
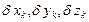– элементарные приращения координат (их вариации) k -й точки системы на ее возможном перемещении.
Этот принцип применим и тогда, когда имеются связи с трением. В этом случае силу трения следует считать активной.
Пример. В кулисном механизме, расположенном в горизонтальной плоскости, ползуны А и В могут перемещаться вдоль стержней OD и OE кривошипа 1, жестко соединенных между собой под прямым углом (рис. 12.4, а). Стержень 2 шарнирно связан с ползунами А, В, С. Ползун С движется по направляющим параллельно оси х.
Пренебрегая трением, определить силу Q, уравновешивающую момент М. Дано: AB = AC = 1,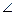 
ABO = 
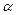, М.
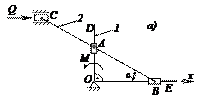Решение. Дадим системе возможное перемещение (рис. 12.4, б). На основании принципа возможных перемещений
,
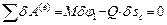где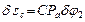 
, 
.
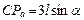Установим связь между возможными перемещениями.
Мгновенный центр вращения тела 2 в движении относительно кривошипа 1 находится в точке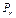 
, а в абсолютном движе-нии – в точке 
.
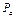Из рис. 12.4 видно, что
, 
.
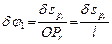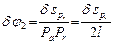Следовательно,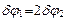 
.
Тогда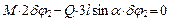 
, откуда 
.
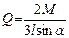Вопрос 41 ПОНЯТИЕ СТЕПЕНИ СВОБОДЫ
Обобщенной силой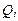 
, соответствующей обобщенной координате 
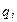, называется скалярная величина, определяемая отношением элементарной работы действующих сил на перемещении системы, вызванном элементарным приращением 
координаты 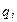, к величине этого приращения 
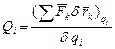. Пусть механическая система состоит из N материальных точек с голономными связями, имеющих n степеней свободы (то есть n обобщенных координат q).
Для равновесия голономной системы с n степенями свободы в ее положении, характеризуемом обобщенными координатами q 1, q 2, …, qn, необходимо и достаточно, чтобы значения всех обобщенных сил, соответствующие значениям обобщенных координат, равнялись нулю.
Date: 2015-09-03; view: 357; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |