Мгновенный центр ускорений

При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение 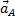какой-нибудь точки А фигуры и величины и 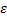, следующим путем:

1) находим значение угла 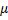, из формулы ;

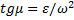2) от точки А под углом 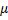, к вектору 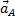проводим прямую АЕ (рис.45);

при этом прямая АЕ должна быть отклонена от 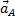в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения ;

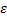3) откладываем вдоль линии АЕ отрезок AQ, равный

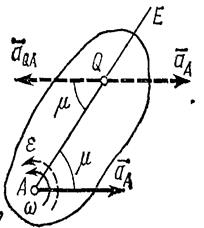
Рис.45

Построенная таким путем точка Q и будет мгно­венным центром ускорений. В самом деле, известно что

,

где численно 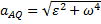. Подставляя сюда значение AQ находим, что 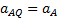. Кроме того, вектор 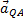должен образовывать с ли­нией AQ угол 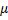, следовательно, вектор 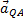параллелен 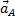, но направлен в про­тивоположную сторону. Поэтому 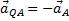и .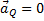

Если точку Q выбрать за полюс, то так как 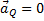, ускорение любой точки М тела, будет

При этом численно

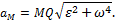
Следовательно, ускорения точек плоской фигуры определяются в данный мо­мент времени так, как если бы движение фигуры, было вращением вокруг мгновенного центра ускорений Q. При этом

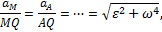
т.е. ускорения точек плоской фигуры пропорциональны их расстояниям от мгно­венного центра ускорений. Картина распределения ускорений точек плоской фигуры в данный момент времени показана на рис.46.

Следует иметь в виду, что положения мгновенного центра скоростей Р и мгно­венного центра ускорений Q в данный момент времени не совпадают. Например, если колесо катится по прямолинейному рельсу (см. рис.47), причем скорость его центра С постоянна (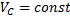), то мгновенный центр скоростей находится в точ­ке Р (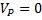), но при этом, как было показано ; следовательно, точка Р не является одновременно мгновенным центром ускорений.

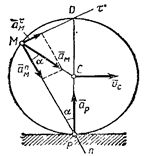
Рис.46 Рис.47

Мгновенный центр ускорений в этом случае находится, очевидно, в точке С, так как она дви­жется равномерно и прямолинейно и 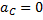. Центры скоростей и ускорений сов­падают тогда, когда фигура (тело) вращается вокруг неподвижной оси.

Понятием о мгновенном центре ускорений удобно пользоваться при решении некоторых задач.

Вопросы для самопроверки

- Какое движение твердого тела называется плоским? Приведите примеры звеньев механизмов, совершающих плоское движение.

- Из каких простых движений складывается плоское движение твердого тела?

- Как определяется скорость произвольной точки тела при плоском движении?

- Какое движение твердого тела называется плоскопараллельным?

- Какими уравнениями задается плоскопараллельное движение?

- Как по уравнениям движения плоской фигуры найти скорость полюса и угловую скорость вращения вокруг полюса?

- Как определить скорость любой точки плоской фигуры?

- Сформулируйте теорему о проекциях скоростей двух точек плоской фигуры.

- Какие способы применяют для определения скоростей точек тела при плоскопараллельном движении?

- Что такое мгновенный центр скоростей? Как определяется величина и направление скорости произвольной точки тела при известном положении мгновенного центра скоростей и угловой скорости?

- Из каких составляющих складывается ускорение точки при плоском движении?

- Запишите формулы для вычисления касательной и нормальной составляющих относительного ускорения точки при плоском движении тела.

- Приведите определение мгновенного центра ускорений.

- При плоском движении тела в некоторый момент времени оказалось, что его точки А и В отстоят от мгновенного центра ускорений на расстояниях 5 и 10 см. Чему равен модуль ускорения точки В, если модуль ускорения точки А равен 3 м/с²?

- Зависят ли поступательное перемещение плоской фигуры и ее поворот от выбора полюса?

- Как определяется скорость любой точки плоской фигуры?

- Покажите, что проекции скоростей точек неизменяемого отрезка на ось, совпадающую с этим отрезком, равны между собой.

- Что представляет собой отрезок, соединяющий две вершины плана скоростей?

- Какие минимальные данные необходимы для построения плана скоростей?

- Какую точку плоской фигуры называют называют мгновенным центром скоростей и каковы основные случаи определения его положения?

- Что представляет собой распределение скоростей точек плоской фигуры в данный момент?

- Как построить центр поворота плоской фигуры, зная ее начальное и конечное положения?

- Что представляет собой неподвижная и подвижная центроиды и что происходит с центроидами при действительном движении плоской фигуры?

- Как определяется ускорение любой точки плоской фигуры?

- Сформулируйте теорему об ускорениях точек плоской фигуры.

- Почему проекция ускорения любой точки плоской фигуры на ось, проходящую через эту точку из полюса, не может быть больше проекции ускорения полюса на эту ось?

- Какую точку плоской фигуры называют мгновенным центром ускорений и может ли мгновенный центр ускорений совпадать с мгновенным центром скоростей?

- Перечислите известные вам способы определения положения мгновенного центра ускорений?

- Что представляет собой картина распределения ускорений точек плоской фигуры в данный момент времени в трех случаях

а) ;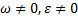

б) ;

в) .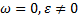

- Как производят определение ускорений точек и угловых ускорений звеньев плоского механизма?

Date: 2015-09-03; view: 768; Нарушение авторских прав